Cho ∆ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I. a) Tứ giác AMCK là hình gì? b) Tứ giác AKMB là hình gì? c) Có trường hợp nào của ∆
30
12/05/2024
Cho ∆ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.
a) Tứ giác AMCK là hình gì?
b) Tứ giác AKMB là hình gì?
c) Có trường hợp nào của ∆ABC để tứ giác AKMB là hình thoi không? Vì sao?
Trả lời
Lời giải
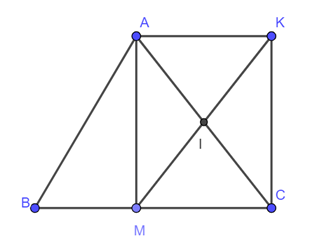
a) Áp dụng tính chất của ∆ cân cho DABC ta có: AM ⊥ MC và BM = MC
Vì I là trung điểm của AC và K đối xứng với M qua I nên tứ giác AMCK là hình bình hành.
Lại có MK = AC (= 2MI).
Do đó, tứ giác AMCK là hình chữ nhật.
b) Vì tứ giác AMCK là hình chữ nhật (theo câu a).
Do đó AK // MC và AK = MC = MB.
Vậy tứ giác AKMB là hình bình hành.
c) Nếu tứ giác AKMB là hình thoi thì BA = AK = KM = MB.
Vì DMBA cân tại B nên \[\widehat {BAM} = \widehat {AMB}\] = 90° (vô lí).
Vậy không có trường hợp nào của DABC để AKMB là hình thoi.

