Cho ∆ABC cân tại A. H là trung điểm của BC. D là hình chiếu của H trên AC
Cho ∆ABC cân tại A. H là trung điểm của BC. D là hình chiếu của H trên AC, M là trung điểm của HD. Chứng minh AM vuông góc BD.
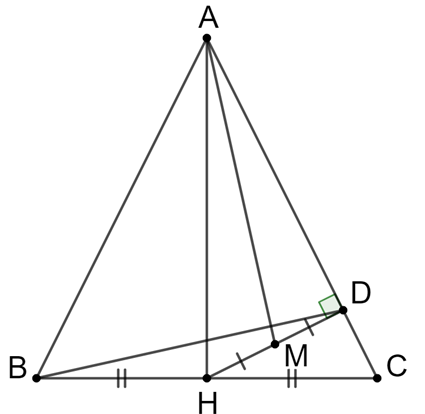
Tam giác ABC cân tại A, H là trung điểm của BC nên AH ^ BC.
Ta có: \(\overrightarrow {AM} \,.\,\overrightarrow {BD} = \frac{1}{2}\left( {\overrightarrow {AH} + \overrightarrow {AD} } \right)\left( {\overrightarrow {BH} + \overrightarrow {HD} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AH} \,.\,\overrightarrow {BH} + \overrightarrow {AH} \,.\,\overrightarrow {HD} + \overrightarrow {AD} \,.\,\overrightarrow {BH} + \overrightarrow {AD} \,.\,\overrightarrow {HD} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AH} \,.\,\overrightarrow {HD} + \overrightarrow {AD} \,.\,\overrightarrow {BH} } \right)\) (Do AH ^ BC và HD ^ AC)
\( = \frac{1}{2}\overrightarrow {AH} \,.\,\overrightarrow {HD} + \frac{1}{2}\left( {\overrightarrow {AH} + \overrightarrow {HD} } \right)\overrightarrow {BH} \)
\( = \frac{1}{2}\overrightarrow {AH} \,.\,\overrightarrow {HD} + \frac{1}{2}\overrightarrow {AH} \,.\,\overrightarrow {BH} + \frac{1}{2}\overrightarrow {HD} \,.\,\overrightarrow {BH} \)
\( = \frac{1}{2}\overrightarrow {AH} \,.\,\overrightarrow {HD} + \frac{1}{2}\overrightarrow {HD} \,.\,\overrightarrow {BH} \) (Do AH ^ BC)
\( = \frac{1}{2}\overrightarrow {HD} \left( {\overrightarrow {AH} + \overrightarrow {BH} } \right)\)
\( = \frac{1}{2}\overrightarrow {HD} \left( {\overrightarrow {AH} + \overrightarrow {HC} } \right)\) (Do M là trung điểm của BC)
\( = \frac{1}{2}\overrightarrow {HD} \,.\,\overrightarrow {AC} = 0\)
Vậy AM vuông góc với BD