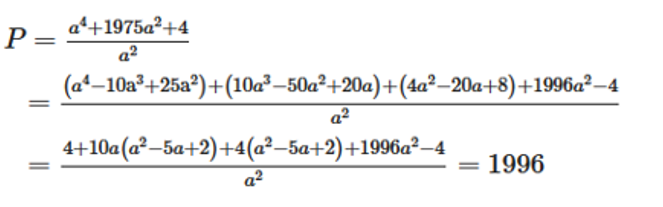Cho a thỏa mãn a² – 5a + 2 = 0. Tính giá trị của biểu thức:

P = a⁵ – a⁴ – 18a³ + 9a² – 5a + 2017 + (a⁴ – 40a² + 4) : a².

Đáp án đúng là: C

Ta có:

P = a⁵ – a⁴ – 18a³ + 9a² – 5a + 2017 + (a⁴ – 40a² + 4) : a²

P = (a⁵ – 5a⁴ + 2a³) + (4a⁴ – 20a³ + 8a²) + (a² – 5a + 2) + 2015 + (a⁴ – 40a² + 4) : a²

P = a³(a² – 5a + 2) + 4a²(a² – 5a + 2) + (a² – 5a + 2) + 2015 + (a⁴ – 40a² + 4) : a²

P = a³ . 0 + 4a² . 0 + 0 + 2015 + (a⁴ – 40a² + 4) : a²

^{$P=2015+\frac{a^4-40{\text{a}}^2+4}{a^2}$}

^{$P=\frac{a^4-40{\text{a}}^2+4+2015{\text{a}}^2}{a^2}=\frac{a^4+1975a^2+4}{a^2}$}

Vì a² – 5a + 2 = 0

⇔ a² – 5a = –2

⇔ (a² – 5a)² = 4

⇔ a⁴ – 10a³ + 25a² = 4

Nên ta có:

Vậy ta chọn đap án C.