Cho a, b, c là ba cạnh của một tam giác. Chứng minh rằng: A = a/b + c - a + b/a + c - b + c/a + b - c lớn hơn bằng 3
Cho a, b, c là ba cạnh của một tam giác. Chứng minh rằng:
A=ab+c−a+ba+c−b+ca+b−c≥3.
Cho a, b, c là ba cạnh của một tam giác. Chứng minh rằng:
A=ab+c−a+ba+c−b+ca+b−c≥3.
Lời giải
Vì a, b, c là ba cạnh của một tam giác
Nên ab+c−a>0,ba+c−b>0,ca+b−c>0
Ta có:
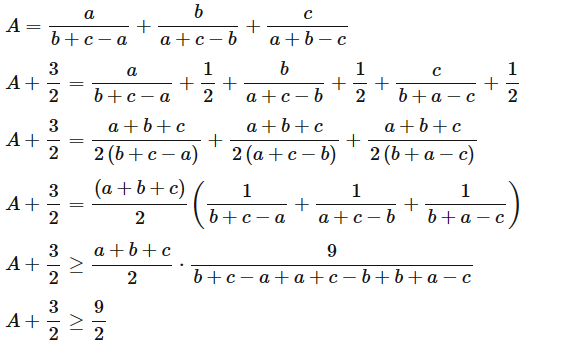
Hay A ≥ 3
Vậy A ≥ 3.