Cho a, b, c > 0. Chứng minh rằng: 1/a^2 + bc + 1/b^2 + ac + 1/c^2 + ab nhỏ hơn bằng a + b + c/2abc
Cho a, b, c > 0. Chứng minh rằng:
1a2+bc+1b2+ac+1c2+ab≤a+b+c2abc
Cho a, b, c > 0. Chứng minh rằng:
1a2+bc+1b2+ac+1c2+ab≤a+b+c2abc
Lời giải
Áp dụng bất đẳng thức Cô – si ta có:
![]()
Do đó:
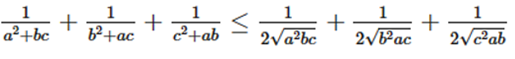
1a2+bc+1b2+ac+1c2+ab≤√bc+√ac+√ab2abc (*)
Áp dụng bất đẳng thức Cô – si ta có:
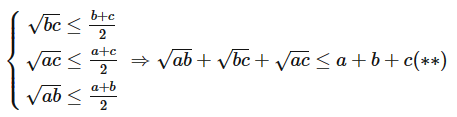
Từ (*) và (**) suy ra
1a2+bc+1b2+ac+1c2+ab≤a+b+c2abc
Vậy 1a2+bc+1b2+ac+1c2+ab≤a+b+c2abc với a, b, c > 0.