Cho 4 điểm A, B, C, D bất kì. a) Chứng minh: vecto DA . vecto BC + vecto DB
Cho 4 điểm A, B, C, D bất kì.
a) Chứng minh: →DA.→BC+→DB.→CA+→DC.→AB=→0.
b) Từ đó suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng qui".
a) →DA.→BC+→DB.→CA+→DC.→AB
=→DA.(→DC−→DB)+→DB.→CA+→DC.→AB
=→DA.→DC−→DA.→DB+→DB.→CA+→DC.→AB
=(→DA+→AB).→DC−(→CA−→DA.)→DB
=→DB.→DC−→DB.→DC
=→0.
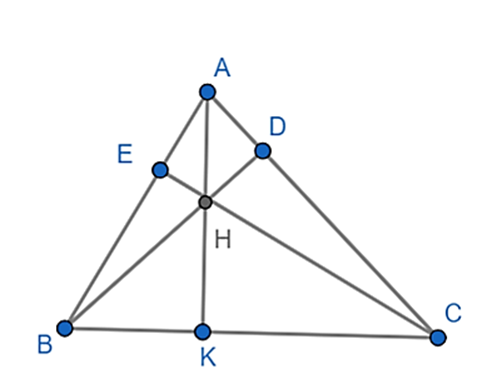
b) Xét tam giác ABC
Gọi BD và CE là đường cao của tam giác ABC
Gọi H là giao điểm của BD và CE
Theo chứng minh câu a, ta có phương trình đúng sau, với 4 điểm A,B,C,H
→HA.→BC+→HB.→CA+→HC.→AB=→0
Vì BH ⊥ AC và CH ⊥ AB nên:
→HB.→CA=→HC.→AB=→0
Do đó: →HA.→BC=→0
Suy ra: AH ⊥ BC
Vậy 3 đường cao đồng quy tại H.