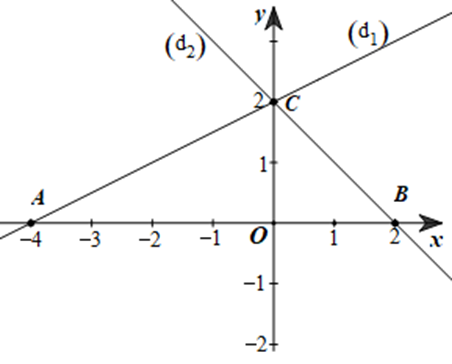
Cho 2 đường thẳng $\left( {{d_1}} \right):y = \frac{1}{2}x + 2$ và (d₂): y = − x + 2. Gọi A, B lần lượt là giao điểm của (d₁) và (d₂) với trục Ox, C là giao điểm của (d₁) và (d₂). Tính chu vi và diện tích tam giác ABC.

Xét phương trình hoành độ giao điểm của (d₁) và (d₂) có

$\frac{1}{2}x + 2 = - x + 2$

$\Leftrightarrow \frac{3}{2}x = 0$

⇔ x = 0

Suy ra y = 2

Khi đó C(0; 2), suy ra CO = |2| = 2.

Giao điểm A của $\left( {{d_1}} \right):y = \frac{1}{2}x + 2$ và Ox là điểm A(− 4; 0) nên OA = |–4| = 4.

Giao điểm B của (d₂): y = − x + 2 và Ox là điểm B(2; 0) nên OB = |2| = 2.

Ta có AB = OA + OB = 4 + 2 = 6

Diện tích tam giác ABC là ${{\rm{S}}_{ABC}} = \frac{1}{2}.CO.AB = \frac{1}{2}.2.6 = 6$.

Xét DOAC vuông tại O có AC² = OA² + OC²

$\Rightarrow AC = \sqrt {{4^2} + {2^2}} = 2\sqrt 5$.

Xét DOBC vuông tại O có BC² = OB² + OC²

$\Rightarrow BC = \sqrt {{2^2} + {2^2}} = 2\sqrt 2$

Chu vi tam giác ABC là $AB + BC + CA = 6 + 2\sqrt 2 + 2\sqrt 5$.