Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau:

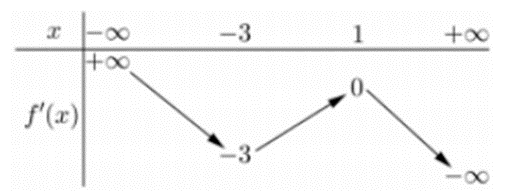
Bất phương trình f(x) < e^x + m đúng với mọi x ∈ (–1; 1) khi và chỉ khi:

A. m ≥ f(1) – e

B. \(m > f\left( { - 1} \right) - \frac{1}{e}\)

C. \(m \ge f\left( { - 1} \right) - \frac{1}{e}\)

D. m > f(1) – e .

Đáp án đúng là: C

Ta có: \(f(x) < {e^x} + m \Leftrightarrow f(x) - {e^x} < m\)

Đặt \(g(x) = f(x) - {e^x}\). Khi đó:

\(\begin{array}{l}f(x) < {e^x} + m;\forall x \in ( - 1;1)\\ \Rightarrow g(x) = f(x) - {e^x} < m;\forall x \in ( - 1;1)\\ \Leftrightarrow m \ge \mathop {max}\limits_{\left[ { - 1;1} \right]} g(x)\end{array}\)

Ta có g’(x) = f’(x) – e^x

Trên (–1; 1) ta có: \(f'(x) < 0;{e^x} > 0;\forall x \in R \Rightarrow g'(x) < 0;\forall x \in ( - 1;1)\)

Suy ra g(x) nghịch biến trên (–1; 1)

Do đó: \(\mathop {max}\limits_{\left[ { - 1;1} \right]} g(x) = g( - 1) = f( - 1) - {e^{ - 1}} = f( - 1) - \frac{1}{e}\)

Suy ra \(m \ge f( - 1) - \frac{1}{e}\)

Vậy đáp án cần chọn là: C.