Câu hỏi:
09/04/2024 38
b) Tại giá trị nào của x thì f(x) có cực đại và cực tiểu? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại và cực tiểu? Giải thích.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
b) Dựa vào bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại x = 2 và x = 6.
Hàm số đạt cực đại tại x = 4.
b) Dựa vào bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại x = 2 và x = 6.
Hàm số đạt cực đại tại x = 4.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giải thích vì sao nếu f'(x) không đổi dấu khi x qua x0 thì x0 không phải là điểm cực trị của hàm số f(x)?
Giải thích vì sao nếu f'(x) không đổi dấu khi x qua x0 thì x0 không phải là điểm cực trị của hàm số f(x)?
Câu 2:
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức : h(t) = 2 + 24,5t – 4,9t2.
Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức : h(t) = 2 + 24,5t – 4,9t2.
Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Câu 3:
Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong hình 1.13.
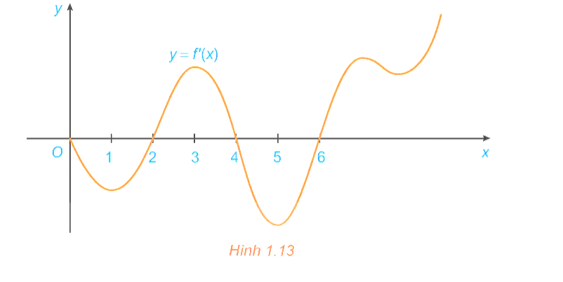
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong hình 1.13.

a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
Câu 4:
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới(trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f'(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Câu 5:
b) Tính đạo hàm N'(t) và . Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
b) Tính đạo hàm N'(t) và . Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Câu 6:
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức s(t) = t3 – 9t2 + 15t, t ³ 0. Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức s(t) = t3 – 9t2 + 15t, t ³ 0. Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Câu 7:
Xét hàm số có đồ thị như hình 1.6
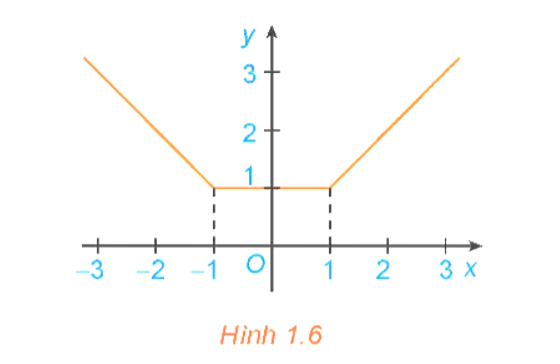
a) Xét dấu đạo hàm của hàm số trên các khoảng (−∞; −1), (1; +∞). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu đạo hàm của hàm số trên mỗi khoảng này.
Xét hàm số có đồ thị như hình 1.6

a) Xét dấu đạo hàm của hàm số trên các khoảng (−∞; −1), (1; +∞). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu đạo hàm của hàm số trên mỗi khoảng này.
Câu 8:
Hình 1.5 là đồ thị của hàm số y = x3 – 3x2 + 2. Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.
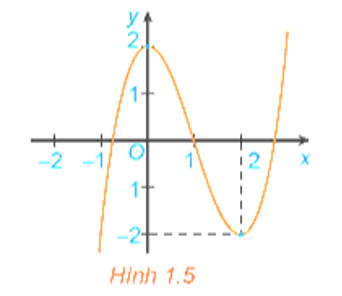
Hình 1.5 là đồ thị của hàm số y = x3 – 3x2 + 2. Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.

Câu 10:
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
Câu 11:
Cho hàm số y = f(x) = x3 – 3x2 + 2x + 1.
a) Tính đạo hàm f'(x) và tìm các điểm x mà f'(x) = 0.
Cho hàm số y = f(x) = x3 – 3x2 + 2x + 1.
a) Tính đạo hàm f'(x) và tìm các điểm x mà f'(x) = 0.
Câu 12:
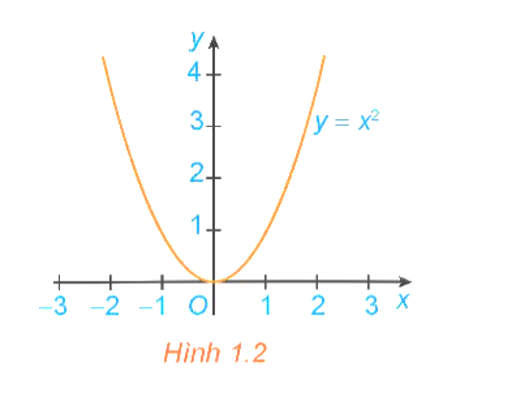
Quan sát đồ thị của hàm số y = x2 (H.1.2)
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?