Câu hỏi:
09/04/2024 75
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3 km và muốn đến điểm B ở bờ đối diện cách 8 km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyền thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6 km/h và vận tốc chạy bộ là 8 km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến được B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).
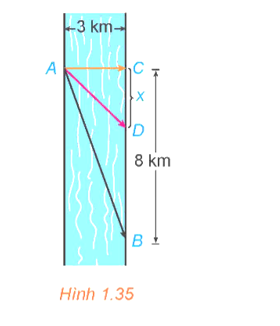
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3 km và muốn đến điểm B ở bờ đối diện cách 8 km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyền thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6 km/h và vận tốc chạy bộ là 8 km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến được B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi độ dài đoạn CD là x (km, 0 ≤ x ≤ 8).
Khi đó độ dài quãng đường AD là (km).
Thời gian đi hết quãng đường AD là: .
Độ dài quãng đường BD là 8 – x (km).
Thời gian đi hết quãng đường BD là: (h).
Thời gian người đó đi đến B bằng cách chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B là .
Bài toán trở thành tìm giá trị nhỏ nhất của hàm số .
Có ;
'
Bảng biến thiên
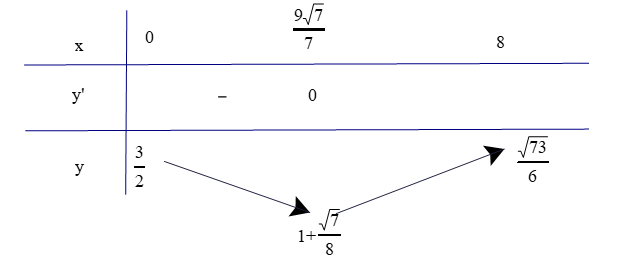
Dựa vào bảng biến thiên ta thấy anh An phải chèo thuyền đến điểm D cách C một đoạn km thì sẽ đến B sớm nhất.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó là: C(x) = 23000 + 50x – 0,5x2 + 0,00175x3.
a) Tìm hàm chi phí biên.
Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó là: C(x) = 23000 + 50x – 0,5x2 + 0,00175x3.
a) Tìm hàm chi phí biên.
Câu 3:
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t (giây) là y = t3 – 12t + 3, t ³ 0.
a) Tìm các hàm vận tốc và gia tốc.
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t (giây) là y = t3 – 12t + 3, t ³ 0.
a) Tìm các hàm vận tốc và gia tốc.
Câu 5:
Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức , trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.
a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức , trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.
a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
Câu 6:
Một đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu để doanh thu từ tiền bán vé là lớn nhất?
Một đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu để doanh thu từ tiền bán vé là lớn nhất?
Câu 7:
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số x = x(p). Từ đồ thị đã vẽ, hãy cho biết:
- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;
- Ý nghĩa thực tiễn của giới hạn .
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số x = x(p). Từ đồ thị đã vẽ, hãy cho biết:
- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;
- Ý nghĩa thực tiễn của giới hạn .
Câu 9:
Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P (tính bằng mmHg) được cho bởi hàm số trong đó thời gian t được tính bằng giây. Tính tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim.
Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P (tính bằng mmHg) được cho bởi hàm số trong đó thời gian t được tính bằng giây. Tính tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim.
Câu 10:
Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
Câu 11:
c) Nếu hàm chi phí hằng tuần là C(x) = 12000 – 3x (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
c) Nếu hàm chi phí hằng tuần là C(x) = 12000 – 3x (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
Câu 12:
b) Khi nào thì hạt chuyển động lên trên và khi nào thì hạt chuyển động xuống dưới.
b) Khi nào thì hạt chuyển động lên trên và khi nào thì hạt chuyển động xuống dưới.
Câu 14:
Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất?
Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất?
Câu 15:
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?

