a) Vẽ đồ thị hàm số y = –x² (P) và hàm số y = –2x – 3 (D) trên cùng hệ tọa độ.

b) Tìm tọa độ giao điểm của (P) và (D).

c) Gọi giao điểm (P) và (D) là A. Tính độ dài từ A đến B(5; –7).

Lời giải

a) Bảng giá trị của hàm số y = –x²:

Bảng giá trị của hàm số y = –2x – 3:

Đồ thị:

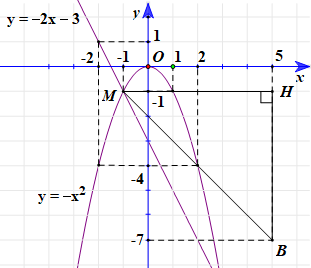
b) Phương trình hoành độ giao điểm của (P) và (D): –x² = –2x – 3

⇔ x² – 2x – 3 = 0

⇔ (x – 3)(x + 1) = 0

⇔ x = 3 hoặc x = –1.

Với x = 3, ta có: y = –3² = –9.

Với x = –1, ta có: y = –(–1)² = –1.

Vậy giao điểm của (P) và (D) là M(–1; –1), N(3; –9).

c) Trường hợp 1: A ≡ M(–1; –1).

Gọi H là giao điểm của hai đường thẳng x = 5 và y = –1.

Suy ra tọa độ H(5; –1).

Ta có: MH = 5 + 1 = 6, BH = 7 – 1 = 6.

Tam giác MBH vuông tại H: MB² = MH² + BH² (Định lí Pytago).

= 6² + 6² = 72.

Suy ra \(MB = 6\sqrt 2 \).

Trường hợp 2: A ≡ N(3; –9).

Ta thực hiện tương tự trường hợp 1, ta được: \(NB = 2\sqrt 2 \).

Vậy độ dài từ A đến B(5; –7) lần lượt là \(6\sqrt 2 \) (khi A(–1; –1)) và \(2\sqrt 2 \) (khi A(3; –9)).