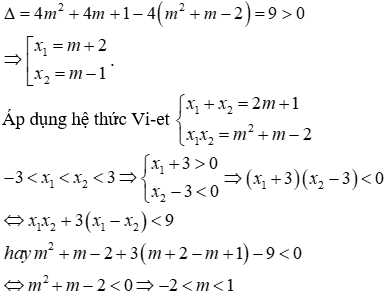1) Giải hệ phương trình sau: căn bậc hai (x + 1) + 1 / (x - y) = 1; căn bậc hai (x + 1)
1) Giải hệ phương trình sau : \(\left\{ \begin{array}{l}\sqrt {x + 1} + \frac{1}{{x - y}} = 1\\\sqrt {x + 1} - \frac{2}{{x - y}} = 4\end{array} \right.\)
2) Cho Parabol \(\left( P \right):y = {x^2}\)và đường thẳng \(\left( d \right):y = \left( {2m + 1} \right)x - {m^2} - m + 2\left( m \right.\)là tham số)
a) Tìm tọa độ giao điểm của \(\left( P \right),\left( d \right)\)với \(m = 3\)
b) Chứng minh rằng đường thẳng \(\left( d \right)\)luôn cắt Parabol \(\left( P \right)\)tại hai điểm phân biệt với mọi giá trị của \(m.\)Gọi \({x_1},{x_2}\)là hoành độ của hai giao điểm đó, tìm \(m\)để \( - 3 < {x_1} < {x_2} < 3\)