Tích vô hướng của một vectơ với một số
Kiến thức cần nhớ
1. Tích vô hướng của vectơ với một số
+) Tích của một vecto với một số thực là một vecto, kí kiệu là
+) Vecto có độ dài bằng và
Cùng hướng với vecto nếu
Ngược hướng với vecto nếu
+) Quy ước:
Nhận xét: Hai vecto và cùng phương khi và chỉ khi tồn tại để
2. Các tính chất của phép nhân vectơ với một số
+) Với hai vecto và hai số thực ta luôn có:
+) Nhận xét:
I là trung điểm của AB
G là trọng tâm
+) Hệ quả
Với M tùy ý thì (I là trung điểm của AB)
Với O tùy ý thì (G là trọng tâm )
Các dạng bài tập Tích vô hướng của một vectơ với một số
Dạng 1. Xác định vectơ ka.
Dạng 2. Hai vectơ cùng phương, ba điểm thẳng hàng.
Dạng 3. Biểu thị một vectơ theo hai vectơ không cùng phương.
Dạng 4. Đẳng thức vectơ chứa tích của vectơ với một số.
Bài tập có hướng dẫn
1. Bài tập vận dụng
1.1. Bài tập trắc nghiệm
Câu 1: Cho vectơ , và hai số thực k, t. Khẳng định nào sau đây là sai?
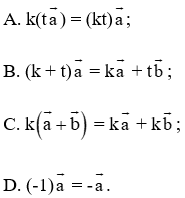
Hướng dẫn giải
Đáp án đúng là B
Ta có (k + t) = k + t . Do đó B sai.
Câu 2: Cho vectơ với số thực k như thế nào thì vectơ ngược hướng với vectơ .
A. k = 1;
B. k = 0;
C. k < 0;
D. k > 0.
Hướng dẫn giải
Đáp án đúng là C
Tích của một vectơ với số thực k < 0 là một vec tơ kí hiệu ngược hướng với vectơ .
Câu 3: Cho ba điểm A, B, C phân biệt sao cho . Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
A. k < 0
B. k = 1
C. 0 < k < 1
D. k > 1
Hướng dẫn giải
Đáp án đúng là D

Vì C là trung điểm của đoạn thẳng AB nên AC = 2AB.
Ta có là hai vectơ cùng hướng nên . Suy ra k = 2 > 1.
Vậy k thỏa mãn điều kiện k > 1.
1.2. Bài tập tự luận
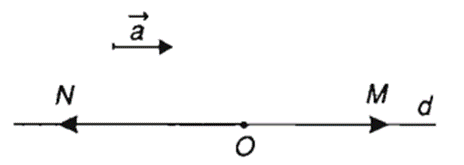
Câu 4: Cho và điểm O không thuộc giá của . Xác định hai điểm M và N sao cho .
Hướng dẫn giải
Vẽ đường thẳng d đi qua O và song song với giá của .
Trên d lấy điểm M sao cho OM= 3||, và cùng hướng khi đó .
Trên d lấy điểm N sao cho ON = 4||, và ngược hướng, khi đó .
Câu 5: Cho tam giác ABC. Hai điểm M, N được xác định bởi các hệ thức: . Chứng minh MN // AC.
Hướng dẫn giải
Vì
Do đó ta có:
Hay
⇔
⇔
Vậy và cùng phương.
Từ giả thiết suy ra , mà A, B, C không thẳng hàng nên bốn điểm A, B, C, M là 4 đỉnh của một hình bình hành.
Suy ra M không thuộc đường thẳng AC, mà và cùng phương.
Vậy MN // AC.
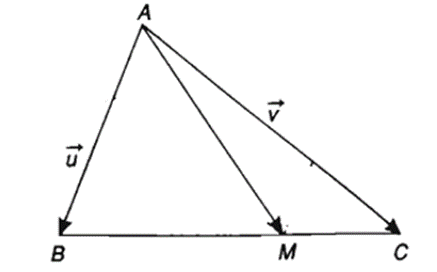
Câu 6: Cho tam giác ABC. Điểm M trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ theo hai vectơ .
Hướng dẫn giải
Ta có:
=
Vậy .
2. Bài tập tự luyện có hướng dẫn
(Xem thêm các bài tập trong file pdf)
Xem thêm các dạng bài tập toán hay khác:
80 Bài tập Tổng và hiệu của hai vectơ (có đáp án năm 2023)
80 Bài tập về vectơ trong mặt phẳng tọa độ (có đáp án năm 2024)
90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2023)
80 Bài tập số gần đúng và sai số (có đáp án năm 2023)
80 Bài tập các số đặc trưng đo độ phân tán (có đáp án năm 2023)