50 Bài tập về quan hệ chia hết và tính chất (có đáp án năm 2024) - Toán 6

Quan hệ chia hết và tính chất

Kiến thức cần nhớ

1. Quan hệ chia hết

Cho hai số tự nhiên a và b (b $\ne$ 0).

Nếu có số tự nhiên k sao cho a = kb thì ta nói a chia hết cho b kí hiệu là a  b.

Nếu a không chia hết cho b ta kí hiệu là a $\cancel{⋮}$ b.

Ví dụ 1. Tìm kí hiệu thích hợp $\left(⋮,\cancel{⋮}\right)$ điền vào chỗ trống:

a) 12 $\boxed{}$2;                               b) 105 $\boxed{}$ 5;                                      c) 26 $\boxed{}$ 4.

Lời giải

a) Ta có 12 = 2.6 nên 12 chia hết cho 2 ta viết 12 $\boxed{⋮}$2.

b) Ta có 105 = 5.21 nên 105 chia hết cho 5 ta viết 105 $\boxed{⋮}$ 5.

c) Ta có 26 không chia hết cho 4 nên ta viết 26 $\boxed{\cancel{⋮}}$ 4.

+ Ước và bội:

Nếu a chia hết cho b, ta nói b là ước của a và a là bội của b.

Ta kí hiệu Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.

Ví dụ 2. Khẳng định sau đây đúng hay sai?

a) 20 chia hết cho 5, 5 là ước của 20 và 20 là bội của 5.

b) 14 chia hết cho 3, 3 là ước của 14 và 14 là bội của 3.

c) 36 chia hết cho 9, 36 là ước của 9 và 9 là bội của 36.

Lời giải

a) Khẳng định a) đúng.

b) Vì 14 không chia hết cho 3 nên khẳng định b sai.

c) 36 chia hết cho 9 là đúng, trong đó 9 là ước của 36 và 36 là bội của 9 nên c sai.

+ Cách tìm ước và bội:

Muốn tìm các ước của a (a > 1), ta lần lượt chia a cho các số tự nhiên từ 1 đến a để xem a chia hết cho những số nào thì các số đó là ước của a.

Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt với 0; 1; 2; 3; …

Ví dụ 3.

a) Hãy tìm tất cả các ước của 12.

b) Hãy tìm tất cả các bội của 8 nhỏ hơn 60.

Lời giải

a) Lần lượt chia 12 cho các số từ 1 đến 12, ta thấy 12 chia hết cho 1; 2; 3; 4; 6; 12 nên Ư(12) = {1; 2; 3; 4; 6; 12}.

b) Lần lượt nhân 8 với 0; 1; 2; 3; 4; 5; … ta được các bội của 8 là: 0; 8; 16; 24; 32; 40; 48; 56; 64; …

Các bội nhỏ hơn 60 của 8 là: 0; 8; 16; 24; 32; 40; 48; 56.

2. Tính chất chia hết của một tổng

+ Tính chất 1

Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

- Nếu a $⋮$ m và b $⋮$ m thì (a + b) $⋮$ m.

- Nếu a $⋮$ m, b $⋮$ m và c $⋮$ m thì (a + b + c) $⋮$ m.

Ví dụ 4. Không thực hiện phép tính, hãy cho biết:

a) 20 + 15 có chia hết cho 5 không. Vì sao?

b) 72 + 18 – 12 có chia hết cho 3 không. Vì sao?

Lời giải

a) Ta có 20 $⋮$ 5 và 15 $⋮$ 5 nên theo tính chất 1 thì tổng (20 + 15) $⋮$ 5.

b) Ta có 72 $⋮$ 3, 18 $⋮$ 3 và 12 $⋮$ 3 nên theo tính chất 1 thì tổng (72 + 18 – 12) $⋮$ 3.

+ Tính chất 2

Nếu có một số hạng của một tổng không chia hết cho một số đã cho, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đã cho.

- Nếu a $⋮$ m và b $\cancel{⋮}$ m thì $\left(a+b\right)\cancel{⋮}m$.

- Nếu a $⋮$ m, b $⋮$ m và c $\cancel{⋮}$ m thì (a + b + c) $\cancel{⋮}$ m.

Chú ý: Hai số không chia hết cho một số đã cho thì chưa chắc tổng của chúng không chia hết cho số đó.

Ví dụ 5. Các phát biểu sau đúng hay sai?

a) 219.7 + 12 chia hết cho 7.

b) 2.3.4.11 + 22 + 45 không chia hết cho 11.

c) 8.12 + 9 chia hết cho 5.

Lời giải

a) Vì 219.7 là tích của 7 với số 219 nên chia hết cho 7 nhưng 12 không chia hết cho 7 nên 219.7 + 12  không chia hết cho 7. Do đó a sai.

b) Vì 2.3.4.11 là tích của 11 với các số 2; 3; 4 nên chia hết cho 11, 22 cũng chia hết cho 11 nhưng 45 không chia hết cho 11 nên 2.3.4.11 + 22 + 45 không chia hết cho 11. Do đó b đúng.

c) Ta có 8.12 không chia hết cho 5, 9 cũng không chia hết cho 5 nhưng tổng 8.12 + 9 = 105 lại chia hết cho 5. Do đó c đúng.

Các dạng bài tập về quan hệ chia hết và tính chất

Dạng 1. Xét tính chia hết của một tổng hoặc một hiệu

Phương pháp:

Áp dụng tính chất 1 và tính chất 2 về sự chia hết của một tổng, một hiệu.

Ví dụ:

a) Ta có: $6⋮3;9⋮3;15⋮3\Rightarrow 6+9+15=30⋮3$

b) Ta có: $75⋮15$ và $12\text{⧸}⋮15$ nên $75+12\text{⧸}⋮15$ và $75-12\text{⧸}⋮15$

c) Ta có: $10⋮5;15⋮5;12\text{⧸}⋮5\Rightarrow 10+15+12=37\text{⧸}⋮5$

Dạng 2. Tìm điều kiện của một số hạng để tổng hoặc hiệu chia hết cho một số nào đó

Phương pháp:

Áp dụng tính chất 1 và tính chất 2 để tìm điều kiện của số hạng chưa biết.

Ví dụ:

Cho tổng $M=105+72+x$ . Để $M$ chia hết cho $3$ thì $x$ phải như thế nào?

Giải:

Vì $105⋮3;72⋮3$ nên để $M=105+72+x$ chia hết cho $3$ thì $x⋮3$.

Dạng 3. Xét tính chia hết của một tích

Phương pháp:

 Áp dụng tính chất: Nếu trong một tích các số tự nhiên có một thừa số chia hết cho một số nào đó thì tích cũng chia hết cho số đó.

Ví dụ:

Nếu $n$ chia hết cho $13$ thì $2n$ cũng chia hết cho $13$.

Bài tập tự luyện (có hướng dẫn)

Bài 1: Hãy tìm các ước của mỗi số sau: 30; 35; 17

Lời giải:

+) Lần lượt chia 30 cho các số tự nhiên từ 1 đến 30, ta thấy 30 chia hết cho 1; 2; 3; 5; 6; 10; 15; 30 nên Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.

+) Lần lượt chia 35 cho các số tự nhiên từ 1 đến 35, ta thấy 35 chia hết cho 1; 5; 7; 35 nên 

Ư(35) = {1; 5; 7; 35}. 

+) Lần lượt chia 17 cho các số tự nhiên từ 1 đến 17, ta thấy 17 chia hết cho 1; 17 nên 

Ư(17) = {1; 17}.

Bài 2: Trong các số sau, số nào là bội của 4? 16; 24; 35

Lời giải:

Vì 16 : 4 = 4, 24 : 4 = 6, 35 : 4 = 8 (dư 3)

Nên 16 ⁝ 4; 24 ⁝ 4; 344

Vậy các số là bội của 4 là: 16; 24.

Bài 3: Tìm các số tự nhiên x, y sao cho:

a) x ∈ B(7) và x < 70

b) y ∈ Ư(50) và y > 5

Lời giải:

a) Lần lượt nhân 7 với 0; 1; 2; 3; 4; 5; … ta được các bội của 7 là: 0; 7; 14; 21; 28; 35; 42; 49; 56; 63; 70;…

Ta được B(7) = {0; 7; 14; 21; 28; 35; 42; 49; 56; 63; 70;…}

Mà x ∈ B(7) và x < 70 nên x ∈ {0; 7; 14; 21; 28; 35; 42; 49; 56; 63}.

b) Lần lượt chia 50 cho các số từ 1 đến 50, ta thấy 50 chia hết cho 1; 2; 5; 10; 25; 50 nên 

Ư(50) = {1; 2; 5; 10; 25; 50}

Mà y ∈ Ư(50) và y > 5 nên y ∈ {10; 25; 50}.

Bài 4: Không thực hiện phép tính, hãy cho biết tổng nào sau đây chia hết cho 5?

a) 15 + 1 975 + 2 019;

b) 20 + 90 + 2 025 + 2 050.

Lời giải:

a) Vì 15 ⁝ 5; 1975 ⁝ 5 nhưng 20195 nên (15 + 1 975 + 2 019)5

Vậy tổng 15 + 1 975 + 2 019 không chia hết cho 5.

b) Vì 20 ⁝ 5; 90 ⁝ 5; 2025 ⁝ 5; 2050 ⁝ 5 nên (20 + 90 + 2 025 + 2 050) ⁝ 5

Vậy tổng 20 + 90 + 2 025 + 2 050 chia hết cho 5.

Bài 5: Không thực hiện phép tính, hãy cho biết hiệu nào sau đây chia hết cho 8?

a) 100 - 40

b) 80 - 16

Lời giải:

a) Vì 1008 và 40 ⁝ 8 nên (100 – 40)8

Vậy hiệu 100 – 40 không chia hết cho 8.

b) Vì 8 ⁝ 8 và 16 ⁝ 8 nên theo tính chất chia hết của một hiệu thì (80 - 16) ⁝ 8

Vậy hiệu 80 – 16 chia hết cho 8. 

Bài 6: Khẳng định nào sau đây đúng?

a) 219.7 + 8 chia hết cho 7;

b) 8.12 + 9 chia hết cho 3.

Lời giải:

a) Vì 7 ⁝ 7 nên (219.7) ⁝ 7 và 87 do đó (219.7 + 8)7.

b) Vì 12 ⁝ 3nên (8.12) ⁝ 3 và 9 ⁝ 3 do đó (8.12 + 9) ⁝ 3.

Vậy khẳng định b là đúng.

Bài 7: Cô giáo muốn chia đều 40 học sinh để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở (bỏ trống trong trường hợp không chia được)

Lời giải:

Ta thấy số học sinh bằng số nhóm nhân với số người ở một nhóm (Số người, số nhóm đều là số tự nhiên khác 0)

Do đó: Số nhóm = Số học sinh : Số người ở một nhóm

            Số người ở một nhóm = Số học sinh : Số nhóm

Ta có bảng sau:

Với số nhóm là 6 thì số người ở một nhóm là: 40 : 6 vì  406 nên bỏ trống.

Bài 8: Đội thể thao của trường có 45 vận động viên. Huấn luyện viên muốn chia thành các nhóm để luyện tập sao cho mỗi nhóm có ít nhất 2 người và không quá 10 người. Biết rằng các nhóm có số người như nhau, em hãy giúp huấn luyện viên chia nhé.

Lời giải:

Gọi số người mỗi nhóm được chia là x (người)

Ta có mỗi nhóm có ít nhất 2 người và không quá 10 người nên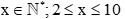 

Vì đội thể thao của trường có 45 vận động viên và huấn luyện viên chia thành các nhóm mà mỗi nhóm có số người như nhau nên 45 ⁝ x hay x ∈ Ư(45) 

Ta lại có Ư(45) = {1; 3; 5; 9; 15; 45}

Mà 2 ≤ x ≤ 10 do đó x ∈ {3; 5; 9}

Với số người mỗi nhóm được chia là 3 người thì số nhóm là: 45 : 3 = 15 (nhóm)

Với số người mỗi nhóm được chia là 5 người thì số nhóm là: 45 : 5 = 9 (nhóm)

Với số người mỗi nhóm được chia là 9 người thì số nhóm là: 45 : 9 = 5 (nhóm)

Vậy huấn luyện viên có thể chia thành 15 nhóm, 9 nhóm hoặc 5 nhóm

Bài 9: 

a) Tìm x thuộc tập {23; 24; 25; 26} biết 56 - x chia hết cho 8

b) Tìm x thuộc tập {22; 24; 45; 48} biết 60 + x không chia hết cho 6

Lời giải:

a) Vì 56 - x chia hết cho 8 mà 56 chia hết cho 8 nên theo tính chất chia hết của một hiệu thì x chia hết cho 8

Mà x thuộc tập {23; 24; 25; 26}, trong các số đó, chỉ có số 24 chia hết cho 8 nên x = 24

Vậy x ∈ 24 .

b) Vì 60 + x không chia hết cho 6 mà 60 chia hết cho 6 nên x không chia hết cho 6

Mà x thuộc tập {22; 24; 45; 48}, trong các số đó thì có hai số 22 và 45 không chia hết cho 6 nên x = 22 hoặc x = 45

Vậy x ∈ { 22;45 }.