Giải Tin học 11 Bài 3: Thực hành về tệp, mảng và danh sách
Nhiệm vụ 1 trang 97 Tin học 11: Lát cắt
b là một phần tử kể từ đầu trái của a
b là các phần tử chỉ số lẻ của a
Hai phần tử đầu tiên của hàng đầu tiên của a
Lời giải:
Toán tử lát cắt (hình 2) trích ra đoạn con liền mạch hay dãy con (có bước nhảy step cách quãng) từ một dãy tuần tự nhiều mục dữ liệu, ví dụ như một biến kiểu danh sách
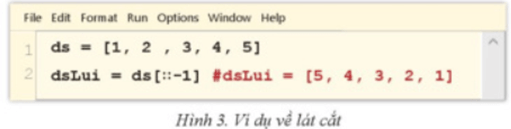
Lưu ý: Nếu bước nhảy step nhận giá trị âm thì toán tử lát cắt sẽ đảo chiều, đi từ cuối danh sách lên đầu danh sách, từ phải sang trái, kết quả nhận được giống như dùng phương thức reverse() (xem ví dụ hình 3).
Nhiệm vụ 2 trang 98 Tin học 11: Vòng lặp
Cho a là mảng hai chiều hình vuông gồm n hàng và n cột các số thực. Hãy tính:
a. Tính tổng các phần tử chỉ số chẵn ở hàng I của a
b. Tổng các phần tử âm, tổng các phẩn tử không âm ở hàng i của a
c. In ra chỉ số các phần tử bằng số x cho trước.
Lời giải:
Vòng lặp for hoặc while duyệt qua các phần tử trong danh sách a và thân vòng lặp có thể xử lí lần lượt tất cả các phần tử hoặc chọn một số phần tử thoả mãn điều kiện nào đó: theo chỉ số i hoặc theo giá trị a(i)
Nhiệm vụ 3 trang 98 Tin học 11: Đọc dữ liệu từ tệp đầu vào và viết ra tệp
Cho tệp “bangDiem.txt" gồm nhiều dòng; các mục dữ liệu cách nhau khoảng trống:
- Dòng thứ nhất: Hai số nguyên dương n và m; với n là số học sinh, m là số môn học.
- Dòng thứ hai: TênHS Toán Văn Tin Li... gồm (m+1) từ.
- n dòng tiếp theo, mỗi dòng có tên học sinh và điểm các môn học của học sinh đó.
a) Một mảng hai chiều n x m các số thực.
b) Hai danh sách: danh sách tên học sinh và danh sách tên môn học.
Lời giải:
Có thể tạo tệp “bangDiem.txt" bằng cách chỉnh sửa và bổ sung bảng trong Hình la ở Bài 2; từ Word hay Excel, thao tác Copy\Paste vào cửa sổ của Notepad hay cửa sổ soạn thảo của Python; ghi lưu thành tệp có định dạng text.
- Đọc từng dòng của tập đầu vào.
- Chuyển đổi mỗi mục của danh sách sang kiểu dữ liệu cần thiết và nối thêm vào
danh sách tương ứng trong chương trình (tham khảo chương trình ở Hình 4).
Trong Python, nếu một dòng gồm nhiều mục khác kiểu dữ liệu, xen kẽ nhau, thì phải truy cập từng phần tử của danh sách và chuyển từ xâu kí tự thành kiểu dữ liệu đúng mô tả.
Các thao tác với tệp dữ liệu
Đầu vào là tệp thuần văn bản chữ và số (đuôi tên tệp “txt”) gồm nhiều dòng; mỗi dòng gồm nhiều từ, mỗi từ là một mục dữ liệu, phân cách bằng khoảng trống.
Các bước thực hiện như sau:
Bước 1. Mở tệp để đọc hay viết, sử dụng hàm open () như ví dụ ở Hình 5.
Bước 2. Đọc từ tệp, có thể dùng các phương thức read(), readline(), readlines() kết hợp với split():
read().split() : Đọc từng từ và nối liền toàn bộ các dòng thành một danh sách các từ. Sử dụng khi tệp ngắn và cần xử lí toàn bộ nội dung tệp.
readline().split() : Đọc một dòng, trả về danh sách các từ, thường dùng nhất. readlines() : Đọc toàn bộ tệp, trả về danh sách các dòng, mỗi dòng là một xâu kí tự, kết thúc bằng ‘\n (dấu xuống dòng).
Bước 3. Xuất ra tệp thuần văn bản: có thể dùng hàm print, sau khi đã chuyển đầu ra chuẩn từ màn hình sang tệp đã mở để viết vào như sau:
Bước 4. Đóng tệp, dùng phương thức close().
Lưu ý: Nếu giữa các từ được phân cách nhau bằng dấu phẩy thì ta có tệp kiểu “csv” (comma separated value) và cần dùng split(',') thay vì dạng mặc định split(). Cần chuyển thành kiểu danh sách (hay mảng) nên sẽ kết hợp xử lí bằng split(',').
Vận dụng
a. Tìm mean của a và đếm số phần tử bé hơn, bằng, lớn hơn mean.
b. Tìm mean của a và cho biết đó là phần tử nào hay nó ở giữa hai phần tử nào.
c. Tìm mode của a và cho biết số lần xuất hiện và dãy các chỉ số tương ứng.
d. Áp dụng để phân tích dãy điểm từng môn học của lớp 11A.
Lời giải:
a) Gợi ý:
import numpy as np
a = np.array([[1, 2], [3, 4]])
b=np.mean(a)
b
x = np.array([[5, 6], [7, 34]])
y=np.mean(x)
y
b) edian hay còn gọi là trung vị (vị trí chính giữa ). Để tìm ra median của dãy trên chúng ta làm như sau:
Sắp xếp dãy trên theo thứ tự tăng dần, 1, 3, 4, 4, 4, 8, 9, 15. Meadian ở đây chính bằng 4.
c)
Hãy xét ví dụ sau {1, 2, 2, 3, 3, 3, 4, 4, 5}. Nếu chúng ta vẽ đồ thị sự phân phối của tập dữ liệu này, chúng ta sẽ được một đường cong đối xứng có chiều cao là 3 tại x = 3 và giảm xuống 1 tại x = 1 và x = 5. Vì 3 là giá trị thường xuyên nhất, nó là mode. Vì giá trị giữa 3 của tập hợp có 4 giá trị ở hai bên nên 3 còn là median. Cuối cùng, giá trị trung bình của tập hợp là 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3, có nghĩa rằng 3 còn là mean.
Ngoại lệ cho quy tắc này là các tập dữ liệu đối xứng có nhiều hơn một mode - trong trường hợp này, vì chỉ có duy nhất một median và mean cho tập dữ liệu đó nên cả hai mode này sẽ không trùng với các điểm kia.
d) Áp dụng để phân tích
Xem thêm lời giải bài tập Tin học lớp 11 sách Cánh diều hay, chi tiết khác: