50 Bài tập về bài tập cuối chương 1 (có đáp án năm 2023) - Toán 6

Kiến thức cần nhớ

I. Tập hợp

1. Tập hợp và phần tử của tập hợp

Tập hợp là một khái niệm cơ bản của toán học (không định nghĩa).

Tập hợp được kí hiệu là các chữ cái in hoa: A, B, C, D, …

2. Mô tả một tập hợp

2.1. Liệt kê các phần tử của tập hợp

Viết tất cả các phần tử của tập hợp trong dấu {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.

2.1. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp

Gọi x là phần tử của tập hợp, tìm các tính chất đặc trưng của các phần tử.

II. Cách ghi số tự nhiên

1. Hệ thập phân

Cách ghi số tự nhiên trong hệ thập phân

- Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng một dãy những chữ số lấy trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 và 9; vị trí của các chữ số trong dãy gọi là hàng.

- Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó. Chẳng hạn, 10 chục thì bằng 1 trăm; 10 trăm thì bằng 1 nghìn; …

Chú ý: Khi viết các số tự nhiên ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên (từ trái sang phải) khác 0.

2. Để dễ đọc với các số có bốn chữ số ta viết tách riêng từng lớp. Mỗi lớp là một nhóm ba chữ số kể từ phải sang trái.

Mỗi số tự nhiên viết trong hệ thập phân đều biểu diễn được thành tổng giá trị các chữ số của nó.

2. Số La Mã

Để viết các số La Mã không quá 30, ta dùng các kí tự I, V và X (gọi là những số La Mã).

Ba chữ số đó cộng với hai cụm chữ số là IV và Ĩ là năm thành phần dùng để ghi số La Mã.

Giá trị của mỗi thành phần được ghi lại trong bảng sau và không thay đổi dù đứng ở bất kì vị trí nào:

+ Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10:

+ Để biểu diễn các số từ 11 đến 20, ta thêm X vào bên trái mỗi số từ I đến X:

+ Để biểu diễn các số từ 21 đến 30, ta thêm XX vào bên trái mỗi số từ I đến X:

III. Thứ tự trong tập hợp các số tự nhiên

Ta đã biết tập các số tự nhiên được kí hiệu là $\mathbb{N}$, nghĩa là $\mathbb{N}=\left\{0;1;2;3;\mathrm{...}\right\}$. Mỗi phần tử 0; 1; 2; 3; … được biểu diễn bởi một điểm trên tia số gốc 0 như hình vẽ:

Trong hai số tự nhiên khác nhau, luôn có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì trên tia số nằm ngang điểm a nằm bên trái điểm b. Khi đó, ta viết a < b hoặc b > a. Ta còn nói: điểm a nằm trước điểm b, hoặc điểm b nằm sau điểm a.

Mỗi số tự nhiên có đúng một số liền sau, chẳng hạn 9 là số liền sau của 8 (còn 8 là số liền trước của 9). Hai số 8 và 9 là hai số tự nhiên liên tiếp.

Nếu a < b và b < c thì a < c (tính chất bắc cầu). Chẳng hạn a < 5 và 5 < 7 suy ra a < 7.

Kí hiệu $"\le "$ và $"\ge "$

Ta còn dùng kí hiệu $a\le b$ (đọc là “a nhỏ hơn hoặc bằng b”) để nói “a < b hoặc a = b”.

Ta còn dùng kí hiệu $a\ge b$ (đọc là “a lớn hơn hoặc bằng b”) để nói “a > b hoặc a = b”.

Tính chất bắc cầu còn có thể viết: nếu  $a\le b$ và $b\le c$ thì $a\le c$.

IV. Phép cộng và phép trừ số tự nhiên

1. Phép cộng số tự nhiên

Phép cộng hai số tự nhiên a và b cho ta một số tự nhiên gọi là tổng của chúng, kí hiệu là a + b.

Có thể minh họa phép cộng nhờ tia số, chẳng hạn phép cộng 3 + 4 = 7

Phép cộng số tự nhiên có các tính chất:

Giáo hoán: a + b = b + a.

Kết hợp: (a + b) + c = a + (b + c).

Chú ý: a + 0  = 0 + a = a.

Tổng (a + b) + c hay a + (b + c) gọi là tổng của ba số a, b, c và viết gọn là: a + b + c.

2. Phép trừ số tự nhiên

Với hai số tự nhiên a, b đã cho, nếu có số tự nhiên c sao cho a + b = c thì ta có phép trừ

a – b = c.

Trong đó, a là số bị trừ, b là số trừ và c là hiệu.

V. Phép nhân và phép chia số tự nhiên

Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích. Kí hiệu: a.b = c (hoặc a x b = c)

Trong đó: a và b là hai thừa số, c là tích.

Chú ý nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …

VI. Lũy thừa với số mũ tự nhiên

Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:

$a^n=\underset{nthöøasoá}{\underbrace{a.a\mathrm{....}a}}\left(n\in {\mathbb{N}}^{*}\right)$

aⁿ đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.

Chú ý: Ta có a¹ = a.

a² cũng được gọi là a bình phương (hay bình phương của a);

a³ cũng được gọi là a lập phương (hay lập phương của a).

VII. Thứ tự thực hiện các phép tính

Đối với các biểu thức không có dấu ngoặc:

- Nếu chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì thực hiện các phép tính từ trái qua phải.

- Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

Đối với các biểu thức có dấu ngoặc:

- Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.

- Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.

Bài tập tự luyện

Bài 1: Viết số tự nhiên a sau đây: Mười lăm tỉ hai trăm sáu mươi bảy triệu không trăm hai mươi mốt nghìn chín trăm linh tám.

a) Số a có bao nhiêu chữ số? Viết tập hợp các chữ số của a

b) Số a có bao nhiêu triệu, chữ số hàng triệu là chữ số nào?

c) Trong a có hai chữ số 1 nằm ở những hàng nào? Mỗi chữ số ấy có giá trị bằng bao nhiêu?

Lời giải:

Số “mười lăm tỉ hai trăm sáu mươi bảy triệu không trăm hai mươi mốt nghìn chín trăm linh tám” được viết là 15 267 021 908.

Vậy số tự nhiên a là 15 267 021 908.

a) Số a có 11 chữ số. Số tự nhiên a viết bởi các chữ số: 1; 5; 2; 6; 7; 0; 2; 1; 9; 0; 8

Chữ số 0 xuất hiện 2 lần, chữ số 1 xuất hiện 2 lần, chữ số 2 xuất hiện 2 lần nhưng trong tập hợp, mỗi phần tử (hay mỗi số) ta chỉ viết (liệt kê) một lần.

Gọi A là tập hợp các chữ số của a.

Do đó tập hợp các chữ số của a là A = {0; 1; 2; 5; 6; 7; 8; 9}.

b) Số a có 267 triệu, chữ số hàng triệu là chữ số 7.

c) Trong a có 2 chữ số 1, tính từ trái qua phải:

+) Chữ số 1 thứ nhất nằm ở hàng chục tỉ có giá trị là: 10 000 000 000

+) Chữ số 1 thứ hai nằm ở hàng nghìn có giá trị là 1 000.

Bài 2: 

a) Số 2 020 là số liền sau của số nào? Là số liền trước của số nào?

b) Cho số tự nhiên a khác 0. Số liền trước của số tự nhiên a là số nào? Số liền sau số tự nhiên a là số nào?

c) Trong các số tự nhiên, số nào không có số liền sau? Số nào không có số liền trước?

Lời giải:

a) Số 2 020 là số liền sau của số 2 019

    Số 2 020 là số liền trước của số 2 021

b) Số liền trước của số tự nhiên a khác 0 là số a – 1. Số liền sau của số tự nhiên a là a + 1

c) Trong các số tự nhiên, không có số nào không có số liền sau. Số 0 không có số liền trước vì trong tập hợp số tự nhiên số 0 là số nhỏ nhất.

Bài 3: Tìm tích, thương và số dư (nếu có):

a) 21 759 . 1 862

b) 3 789 : 231

c) 9 848 : 345

Lời giải:

a)

Do đó: 21 759 . 1 862 = 40 515 258

Vậy ta có tích của phép nhân đã cho là: 40 515 258.

  b) 

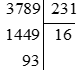
Do đó: 3789 : 231 = 16 (dư 93).

Vậy thương của phép chia trên là 16 và số dư là 93.

c)

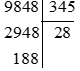
Do đó: 9848 : 345 = 28 (dư 188)

Vậy thương của phép chia trên là 28 và số dư là 188.

Bài 4: Tính giá trị của biểu thức:

 21.[ ( 1245 + 987) : 2³ – 15.12 ] + 21

Lời giải:

21.[ ( 1245 + 987) : 2³ – 15.12 ] + 21

= 21.(2 232 : 8 - 180) + 21

= 21.(279 - 180) + 21

= 21.99 + 21

= 21. 99 + 21. 1 

= 21. (99 + 1)

= 21 . 100

= 2 100.

Bài 5: Khối 6 có 320 học sinh đi tham quan. Nhà trường cần thuê ít nhất bao nhiêu xe ô tô 45 chỗ ngồi để đủ chỗ cho tất cả học sinh?

Lời giải:

Vì 320 : 45 = 7 (dư 5) nên xếp đủ 7 xe thì còn dư 5 học sinh, do đó cần thêm 1 xe để chở hết 5 học sinh đó.

Vậy cần tất cả: 7 + 1 = 8 (xe ô tô).

Bài 6: Một phòng chiếu phim có 18 hàng ghế, mỗi hàng ghế có 18 ghế. Giá một vé xem phim là 50 000 đồng.

a) Tối thứ Sáu, số tiền bán vé thu được là 10 550 000 đồng. Hỏi có bao nhiêu vé không bán được?

b) Tối thứ Bảy, tất cả các vé đều được bán hết. Số tiền bán vé thu được là bao nhiêu?

c) Chủ nhật còn 41 vé không bán được. Hỏi số tiền bán vé thu được là bao nhiêu?

Lời giải:

Số ghế của phòng chiếu phim là:

    18.18 = 324 (ghế)

Như ta thấy, mỗi ghế sẽ tương ứng với 1 vé xem phim nên số vé nhiều nhất có thể bán được là 324 vé.

a) Số vé bán được trong tối thứ Sáu là:

     10 550 000: 50 000 = 211 (vé)

Số vé không bán được trong tối thứ Sáu là:

     324 – 211 = 113 (vé)

b) Tối thứ Bảy tất cả các vé đều được bán hết do đó tối thứ Bảy bán được 324 vé nên số tiền thu được là:

      50 000. 324 = 16 200 000 (đồng)

c) Chủ nhật còn 41 vé không bán được, nên số vé đã bán là:

     324 - 41 = 283 (vé)
    Số tiền bán vé thu được là:

  50 000. 283 = 14 150 000 (đồng)

Vậy: a) Có 113 vé không bán được

         b) Số tiền bán vé thu được là 16 200 000 đồng

         c) Số tiền bán vé thu được là 14 150 000 đồng.