Kiến thức cần nhớ
1. Quy tắc cộng
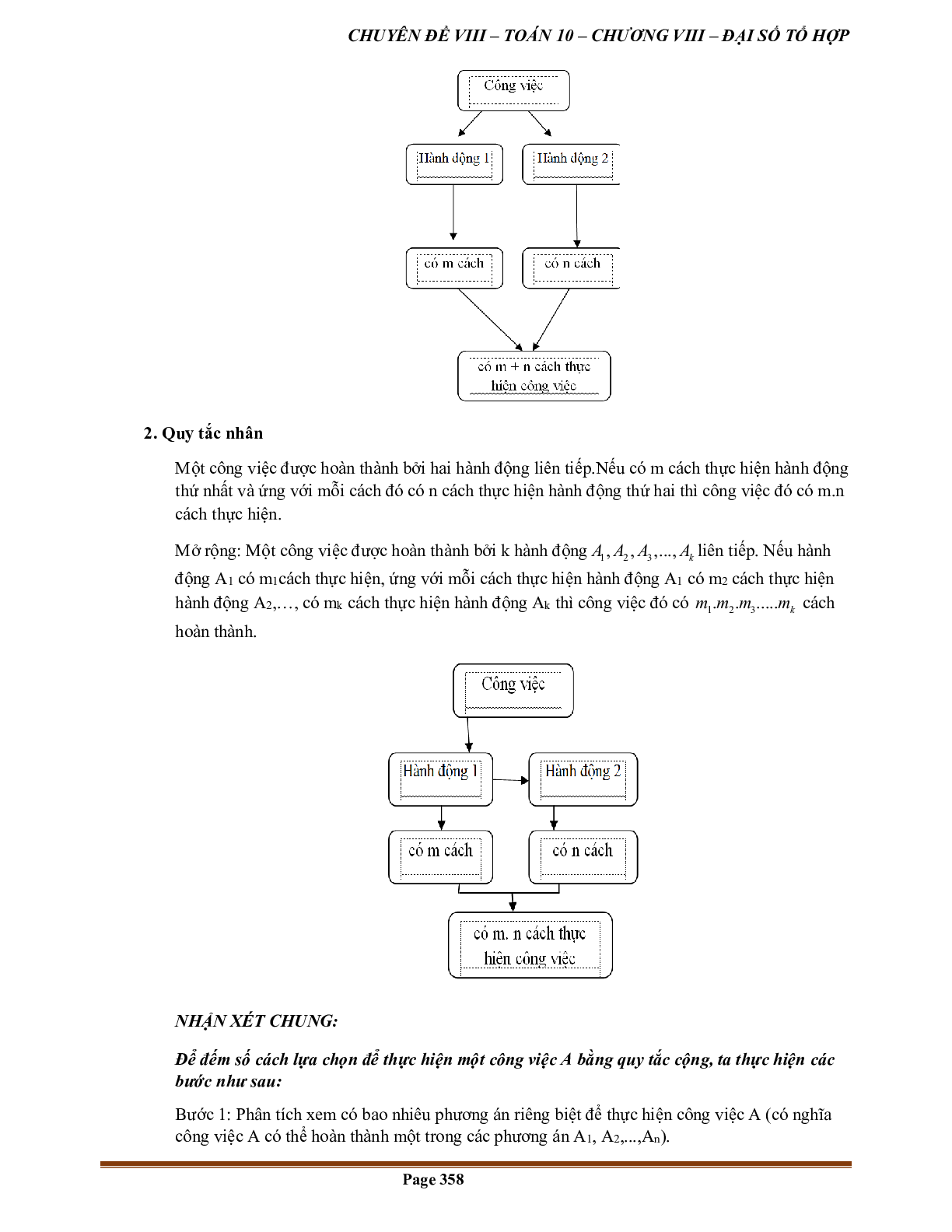
– Giả sử một công việc có thể được thực hiện theo phương án A hoặc B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.
Ví dụ: Lớp 10A có 20 học sinh, lớp 10C có 24 học sinh. Có bao nhiêu cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường?
Hướng dẫn giải
Công việc cử 1 học sinh đi có 2 phương án thực hiện:
Phương án 1: Cử 1 học sinh của lớp 10A, ta có 20 cách.
Phương án 2: Cử 1 học sinh của lớp 10C, ta có 24 cách.
Ta thấy mỗi cách thực hiện của phương án B đều không trùng với cách của phương án A. Do đó theo quy tắc cộng, có 20 + 24 = 44 cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường.
2. Quy tắc nhân
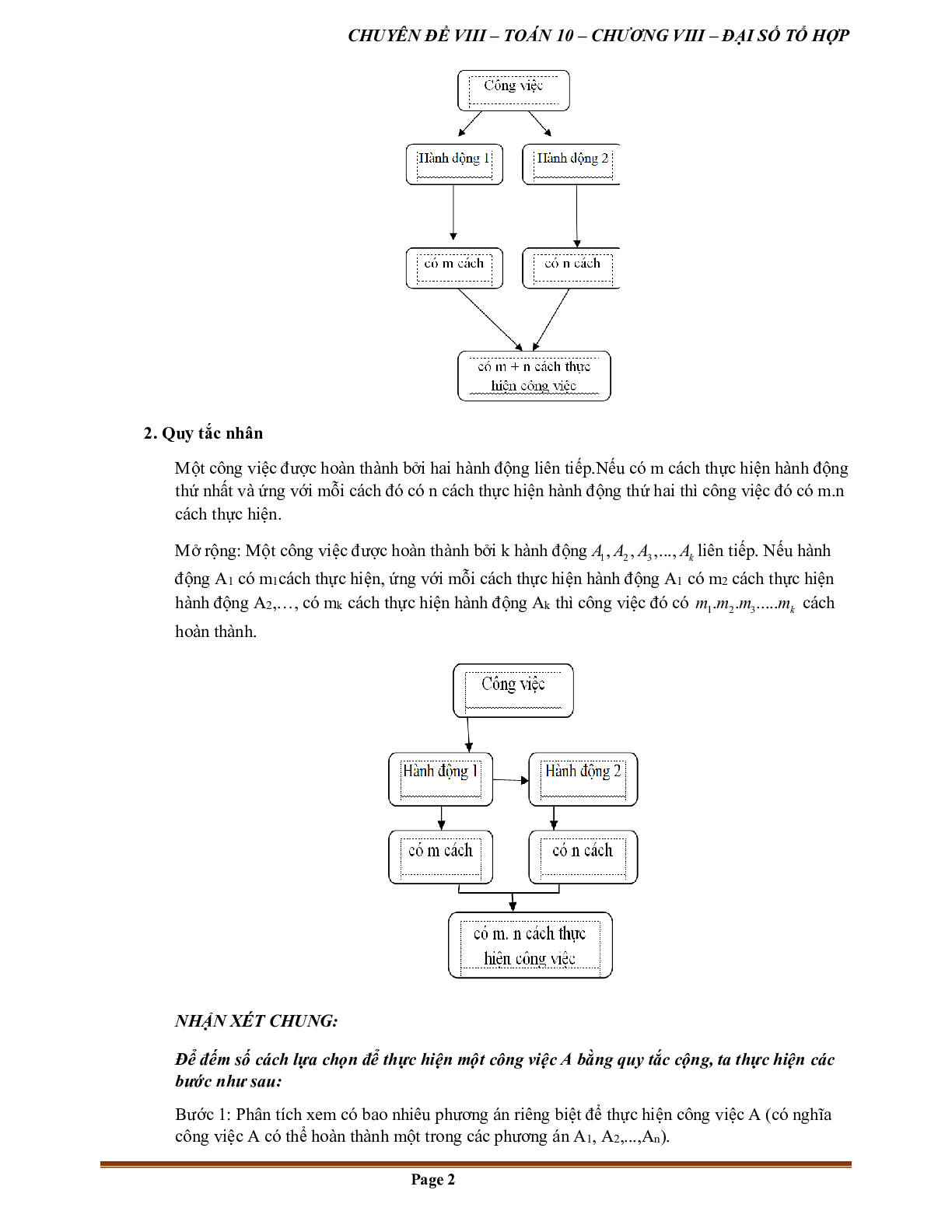
– Giả sử một công việc được chia thành hai công đoạn. Công đoạn thứ nhất có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó công việc có thể thực hiện theo m. n cách.
Ví dụ: Từ nhà An đến trường đi qua 3 điểm A, B, C. Từ nhà An đến điểm A có 3 cách đi, từ điểm A đến điểm B có 4 cách đi, từ điểm B đến điểm C có 2 cách đi. Từ điểm C đến trường học có 2 cách đi. Hỏi có bao nhiêu cách từ nhà An đến trường?
Hướng dẫn giải
Từ nhà An đến trường đi qua 3 điểm A, B, C, như vậy có 4 công đoạn:
+ Công đoạn 1: Từ nhà An đến điểm A có 3 cách đi.
+ Công đoạn 2: Từ điểm A đến điểm B có 4 cách đi
+ Công đoạn 3: Từ điểm B đến điểm C có 2 cách đi.
+ Công đoạn 4: Từ điểm C đến trường học có 2 cách đi.
Do đó, theo quy tắc nhân, có 3. 4. 2. 2 = 48 cách đi từ nhà An đến trường.
Các dạng bài tập quy tắc đếm
Dạng 1. Quy tắc cộng
Phương pháp giải
Nếu một công việc nào nó có thể thực hiện theo n hướng khác nhau, trong đó:
Hướng thứ 1 có m1 cách thực hiện.
Hướng thứ 2 có m2 cách thực hiện.
… …
Hướng thứ n có mn cách thực hiện.
Khi đó, có m1 + m2 + … + mn cách để hoàn thành công việc đã cho.
Dạng 2. Quy tắc nhân
Phương pháp giải
Nếu một công việc nào đó phải hoàn thành qua n giai đoạn liên tiếp, trong đó:
Giai đoạn 1 có m1 cách thực hiện.
Giai đoạn 2 có m2 cách thực hiện.
… …
Giai đoạn n có mn cách thực hiện.
Khi đó, có m1.m2…mn cách để hoàn thành công việc đã cho.
Ta thường gặp các bài toán sau:
Bài toán 1. Đếm số phương án liên quan đến số tự nhiên.
Bài toán 2. Đếm số phương án liên quan đến kiến thức thực tế.
Bài toán 3. Đếm số phương án liên quan đến hình học.
Bài tập tự luyện
1. Bài tập vận dụng
Bài 1. Một giỏ hoa quả chứa 5 quả cam và 4 quả táo.
a) Hỏi có bao nhiêu cách chọn 1 quả cam hoặc 1 quả táo?
b) Hỏi có bao nhiêu cách chọn 1 quả cam và 1 quả táo?
Hướng dẫn giải
a) Chọn 1 quả cam hoặc 1 quả táo, có 2 phương án chọn:
+ Phương án 1: Chọn 1 quả cam trong 5 quả cam có 5 cách.
+ Phương án 2: Chọn 1 quả táo trong 4 quả táo có 4 cách.
Mỗi cách của phương án 2 đều không trùng với cách của phương án 1.
Do đó có 5 + 4 = 9 cách để chọn 1 quả cam hoặc 1 quả táo.
b) Chọn 1 quả cam và 1 quả táo có 2 công đoạn:
+ Công đoạn 1: chọn 1 quả cam có 5 cách.
+ Công đoạn 2: chọn 1 quả táo có 4 cách.
Theo quy tắc nhân, có 5. 4 = 20 cách chọn 1 quả cam và 1 quả táo.
Bài 2. Trong tủ sách của lớp Vân có 10 quyển sách Toán, 5 quyển sách Ngữ Văn và 8 quyển sách Tiếng Anh. Bạn Vân muốn chọn 1 quyển sách Toán, 1 quyển Ngữ Văn và 1 quyển Tiếng Anh để đọc. Hỏi Vân có bao nhiêu cách chọn?
Hướng dẫn giải
Chọn 1 quyển sách Toán, 1 quyển sách Tiếng Việt, 1 sách Tiếng Anh có 3 công đoạn:
+ Công đoạn 1: Chọn 1 quyển Toán có 10 cách.
+ Công đoạn 2: Chọn 1 quyển Ngữ Văn có 5 cách.
+ Công đoạn 3: Chọn 1 quyển Tiếng Anh có 8 cách.
Theo quy tắc nhân, Vân sẽ có 10. 5. 8 = 400 cách chọn 1 quyển sách Toán, 1 quyển sách Ngữ Văn và 1 quyển sách Tiếng Anh.
Bài 3. Có bao nhiêu số tự nhiên có 3 chữ số trong đó:
a) 3 chữ số đều là chữ số chẵn.
b) 2 chữ số hàng chục và hàng trăm là chữ số lẻ, chữ số hàng đơn vị là chữ số chẵn.
Hướng dẫn giải
Gọi số cần tìm có 3 chữ số là ¯abc (với 0 < a < 9; 0 ≤ b, c ≤ 9; a, b, c ∈ ℕ).
Ta có a ∈{1; 2; …; 9}; b ∈{0; 1; 2; …; 9} và c ∈{0; 1; 2; …; 9}.
a) Lập số tự nhiên có 3 chữ số đều là chữ số chẵn có 3 công đoạn:
+ Công đoạn 1: Chọn chữ số hàng trăm: có 4 cách chọn (chọn một trong các chữ số 2; 4; 6; 8).
+ Công đoạn 2: Chọn chữ số hàng chục: có 5 cách chọn (chọn một trong các chữ số 0; 2; 4; 6; 8).
+ Công đoạn 3: Chọn chữ số hàng đơn vị: có 5 cách chọn (chọn một trong các chữ số 0; 2; 4; 6; 8).
Theo quy tắc nhân, có 4. 5. 5 = 100 cách chọn.
Vậy có 100 số tự nhiên có 3 chữ số đều là chữ số chẵn.
b) Lập số tự nhiên theo yêu cầu có 3 công đoạn:
+ Công đoạn 1: Chọn chữ số hàng trăm: có 5 cách chọn (chọn một trong các chữ số 1; 3; 5; 7; 9).
+ Công đoạn 2: Chọn chữ số hàng chục: có 5 cách chọn (chọn một trong các chữ số 1; 3; 5; 7; 9).
+ Công đoạn 3: Chọn chữ số hàng đơn vị: có 5 cách chọn (chọn một trong các chữ số 0; 2; 4; 6; 8).
Theo quy tắc nhân, có 5. 5. 5 = 125 cách chọn.
Vậy có 125 số tự nhiên có 3 chữ số mà 2 chữ số hàng chục và hàng trăm là chữ số lẻ, chữ số hàng đơn vị là chữ số chẵn.
Bài 4. Minh có thể đi từ nhà đến nhà sách theo các con đường như hình vẽ bên dưới, trong đó có những con đường đi qua Circle K và Highlands Coffee.
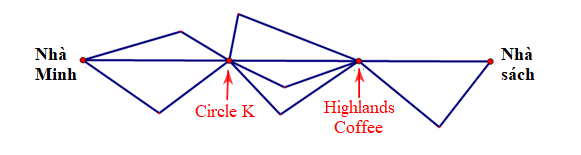
Hỏi Minh có bao nhiêu cách đi từ nhà đến nhà sách?
Hướng dẫn giải
– Đi từ nhà Minh đến nhà sách phải đi qua Circle K và Highlands Coffee có 3 công đoạn:
+ Công đoạn 1: Đi từ nhà Minh đến Circle K: có 3 cách.
+ Công đoạn 2: Đi từ Circle K đến Highlands Coffee: có 4 cách.
+ Công đoạn 3: Đi từ Highlands Coffee đến nhà sách: có 2 cách.
Do đó theo quy tắc nhân có 3. 4. 2 = 24 cách đi từ nhà Minh đến nhà sách.
Vậy có 24 cách đi từ nhà Minh đến nhà sách.