Phương pháp giải bài tập về hằng đẳng thức đáng nhớ (có đáp án năm 2024) - Toán 8

Bài giảng Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ

Lý thuyết

1. Bình phương của một tổng

Bình phương của một tổng bằng bình phương số thứ nhất cộng hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A + B)² = A² + 2AB + B².

Ví dụ 1:

(x + 3)² = x² + 2.x.3 + 3² = x² + 6x + 9.

(2a + b)² = (2a)² + 2.2a.b + b² = 4a² + 4ab + b².

2. Bình phương của một hiệu.

Bình phương của một hiệu bằng bình phương số thứ nhất trừ hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A – B)² = A² – 2AB + B².

Ví dụ 2:

${\left(y-\frac{1}{4}\right)}^2$$=y^2-2.y.\frac{1}{4}+{\left(\frac{1}{4}\right)}^2$$=y^2-\frac{1}{2}y+\frac{1}{16}$

(3x – y)² = (3x)² – 2.3x.y + y² = 9x² – 6xy + y².

3. Hiệu hai bình phương

Hiệu hai bình phương bằng tích của hiệu với tổng của chúng.

Với A, B là các biểu thức tùy ý, ta có: A² –  B² = (A – B)(A + B).

Ví dụ 3:

m² – 4 = m² – 2² = (m – 2)(m + 2)

(2a – b)(2a + b) = (2a)² – b² = 4a² – b²

4. Lập phương của một tổng

Lập phương của một tổng bằng lập phương số thứ nhất cộng ba lần tích của bình phương số thứ nhất nhân số thứ hai cộng ba lần tích của số thứ nhất nhân bình phương số thứ hai cộng lập phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A + B)³ = A³ + 3A²B + 3AB² + B³.

Ví dụ 1:

$$\begin{gathered} {\left(\frac{x}{3}+1\right)}^3 \\ ={\left(\frac{x}{3}\right)}^3+3{\left(\frac{x}{3}\right)}^2.1+3.\frac{x}{3}{.1}^2+1^3 \\ =\frac{x^3}{27}+\frac{x^2}{3}+x+1 \end{gathered}$$

(2m + n)³ = (2m)³ + 3.(2m)².n + 3.2m.n² + n³

= 8m³ + 12m²n + 6mn² + n³.

5. Lập phương của một hiệu

Lập phương của một hiệu bằng lập phương số thứ nhất trừ ba lần tích của bình phương số thứ nhất nhân số thứ hai cộng ba lần tích của số thứ nhất nhân bình phương số thứ hai trừ lập phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A – B)³ = A³ – 3A²B + 3 AB² – B³

Ví dụ 2:

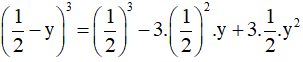
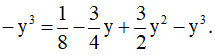
(x² – y)³ = (x²)³ – 3.(x²)².y + 3.x².y² – y³ = x⁶ – 3x⁴y + 3x²y² – y³.

6. Tổng hai lập phương

Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó.

Với A, B là các biểu thức tùy ý, ta có: A³ + B³ = (A + B)(A² – AB + B²)

Chú ý: A² – AB + B² được gọi là bình phương thiếu của một hiệu.

Ví dụ 1:

x³ + 4³ = (x + 4)(x² – 4x + 4²) = (x + 4)(x² – 4x + 16)

$$\begin{gathered} \frac{1}{27}+u^3={\left(\frac{1}{3}\right)}^3+u^3 \\ =\left(\frac{1}{3}+u\right)\left[{\left(\frac{1}{3}\right)}^2-\frac{1}{3}u+u^2\right] \\ =\left(\frac{1}{3}+u\right)\left(\frac{1}{9}-\frac{u}{3}+u^2\right) \end{gathered}$$

7. Hiệu hai lập phương

Hiệu của lập phương hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó.

Với A, B là các biểu thức tùy ý, ta có: A³ – B³ = (A – B)(A² + AB + B²)

Chú ý: A² + AB + B² được gọi là bình phương thiếu của một tổng.

Ví dụ 2:

x³ – (2y)³ = (x – 2y)[x² + 2xy + (2y)²] = (x – 2y)(x² + 2xy + 4y²)

27a³ – 1 = (3a)³ – 1³ = (3a – 1)[(3a)² + 3a.1 + 1²] = (3a – 1)(9a² + 3a + 1)

Các dạng bài tập về những hằng đẳng thức đáng nhớ

A. Bình phương của một tổng, bình phương của một hiệu và hiệu hai bình phương

Dạng 1: Thực hiện phép tính

1. Phương pháp giải

Sử dụng trực tiếp các hằng đẳng thức đã học để khai triển các biểu thức

2. Bài tập minh họa

Ví dụ 1: Thực hiện phép tính:

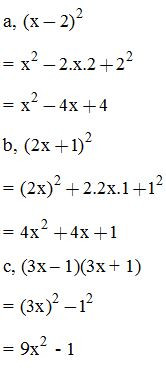
Ví dụ 2: Viết các biểu thức sau dưới dạng bình phương một tổng hoặc bình phương một hiệu:

a. $4x^2+4x+1$

b. $x^2-8x+16$

Hướng dẫn giải

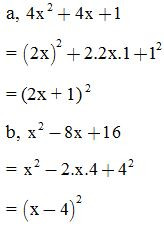
Ví dụ 3: Thực hiện phép tính:

a) (3x+ 2y)²

b) (a + 2b)² + (2a + b)²

c) (1 - 3a)²

d) (x - xy)²

e) (x + y)² – (2 – y)²

f) x² – 4y²

g) 45 . 55

h) 55 . 105

Hướng dẫn giải

a) (3x+ 2y)² = (3x)² + 2.3x.2y + (2y)² = 9x² + 12xy + 4y²

b) (a + 2b)² + (2a + b)² = a² + 2.a.2b + (2b)² + (2a)² + 2.2a.b + b²

= a² + 4ab + 4b² + 4a² + 4ab + b²

= 5a² + 8ab + 5b²

c) (x - xy)² = x² - 2.x.xy + (xy)² = x² - 2x2²y + x²y²

d) (1 - 3a)² = 1² - 2.1.3a + (3a)² = 1 - 6a + 9a²

e) x² – 4y² = x² – (2y)² = (x – 2y).(x + 2y)

f) (x + y)² – (2 – y)²

Cách 1: (x + y)² – (2 – y)²

= (x + y + 2 – y).(x + y – 2 + y)

= (x + 2).(x + 2y – 2)

= x² + 2xy – 2x + 2x + 4y – 4

= x² + 2xy + 4y - 4

Cách 2: (x + y)² – (2 – y)²

= x² + 2xy + y² – (4 – 4y + y²)

= x² + 2xy + y² – 4 + 4y - y²

= x² + 2xy – 4 + 4y

g) 45 . 55 = (50 – 5).(50 + 5) = 50² – 5² = 2500 – 25 = 2475

h) 55 . 105 = (80 – 25).(80 + 25) = 80² – 25² = 6400 – 625 = 5775

Ví dụ 4: Tính nhanh kết quả các biểu thức sau:

a) 127² + 146.127 + 73²

b) 9⁸.2⁸– (18⁴ – 1)(18⁴ + 1)

c) 100² – 99² + 98² – 97² + …+ 2² – 1²

d) (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)

Hướng dẫn giải

a) A = 127² + 146.127 + 73²

= 127² + 2.73.127 + 73²

= (127 + 73)²

= 200²

= 40000 .

b) B = 9 ⁸ .2 ⁸ – (18 ⁴ – 1)(18 ⁴ + 1)

= 18⁸ – (18⁸ – 1)

= 1

c) C = 100² – 99² + 98² – 97² + …+ 2² – 1²

= (100 + 99)(100 – 99) + (98 + 97)(98 – 97) +…+ (2 + 1)(2 – 1)

= 100 + 99 + 98 + 97 +…+ 2 + 1

= 5050.

d) D = (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)

= (20² – 19²) + (18² – 17²) + (16² – 15²)+ …+ (4² – 3²) + (2² – 1²)

= (20 + 19)(20 – 19) + (18 + 17)(18 – 17) + ( 16 +15)(16 – 15)+ …+ (4 + 3)(4 – 3) + (2 + 1)(2 – 1)

= 20 + 19 + 18 + 17 + 16 +15 + …+ 4 + 3 + 2 + 1

= 210

Dạng 2: Tìm x

1. Phương pháp giải

- Sử dụng các hằng đẳng thức và phép nhân đa thức để biến đổi để đưa về dạng tìm x thường gặp.

2. Bài tập minh họa

Ví dụ 1: Tìm x biết

a. 

b. 

c. 

d. 

Hướng dẫn giải

a. 

b.

 

c.

 

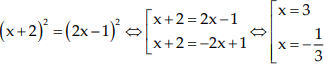
d. 

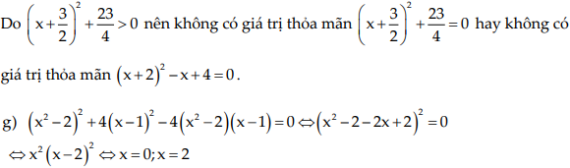
Ví dụ 2: Hiệu các bình phương của 2 số tự nhiên chẵn liên tiếp bằng 36. Tìm hai số ấy.

Hướng dẫn giải

Gọi 2 số chẵn liên tiếp là x và x + 2 (x chẵn). Ta có:

(x + 2)² – x² = 36

$\iff$x² + 4x + 4 – x² = 36

$\iff$4x = 32

$\iff$ x = 8

$\Rightarrow$ số thứ 2 là 8+2 = 10

Đáp số: 8 và 10

Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

1. Phương pháp giải

- Sử dụng hằng đẳng thức để đánh giá các biểu thức đã cho

Với mọi A, B. Dấu “=” xảy ra khi A = -B

Với mọi A, B. Dấu “=” xảy ra khi A = B

2. Bài tập minh họa

Ví dụ 1: Tìm giá trị nhỏ nhất của các biểu thức sau:

a) A = x² – 4x + 1

b) B = 4x² + 4x + 11

c) C = 3x² – 6x – 1

Hướng dẫn giải

a) Ta sẽ biến đổi A= x² – 4x + 1 = x² – 4x + 4 – 3 = ( x- 2)² – 3

Do ( x- 2)² > 0 nên $\Rightarrow$( x- 2)² – 3 ≥ -3

Vậy giá trị nhỏ nhất của biểu thức A(A_min) = -3 khi và chỉ khi x = 2.

b) B = 4x² + 4x + 11 = (2x + 1)² + 10

Vậy B_min = 10 khi và chỉ khi x = $-\frac{1}{2}$

c) C = 3x² – 6x – 1 = 3(x – 1)² – 4

Vậy C_min = -4 khi và chỉ khi x = 1.

Dạng 4: Chứng minh các đẳng thức

1. Phương pháp giải

Áp dụng linh hoạt các hằng đẳng thức, lựa chọn vế có thể dễ dàng áp dụng các hằng đẳng thức. Có thể giải quyết bài toán theo 2 hướng sau:

+ Hướng 1: Khai triển vế trái hoặc vế phải (thường là vế có biểu thức dài hơn) của đẳng thức để biến đổi biểu thức bằng vế còn lại.

+ Hướng 2: Sử dụng hằng đẳng thức biến đổi đồng thời hai vế rồi so sánh kết quả.

2. Bài tập minh họa

Ví dụ 1: Chứng minh các đẳng thức sau:

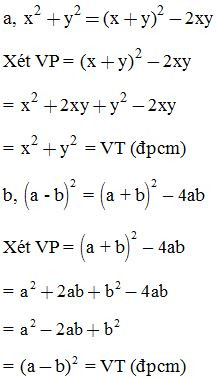
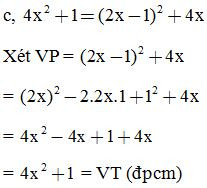
Ví dụ 2: Cho a + b + c = 2p. Chứng minh rằng: 2bc + b² + c² – a² = 4p(p – a)

Hướng dẫn giải

Ta sẽ đi biến đổi VP.

VP = 2p(2p – 2a) = (a + b + c)( a + b – c) = ( b + c )² – a² = b² + 2bc + c² – a² = VT (đccm)

Ví dụ 3: Chứng minh rằng:

a) a(a – 6) + 10 > 0.

b) (x – 3)(x – 5) + 4 > 0.

c) a² + a + 1 > 0.

Hướng dẫn giải

a) VT = a² – 6a + 10 = (a – 3)² + 1 ≥ 1

=> VT > 0

b) VT = x² – 8x + 19 = (x – 4)² + 3 ≥ 3

=> VT > 0

c) a² + a + 1 = a² + 2.a.½ + ¼ + ¾ = (a + ½ )² + ¾ ≥ ¾ >0.

Ví dụ 4: Chứng minh đẳng thức: 

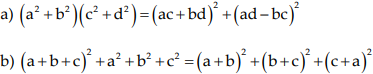
Hướng dẫn giải

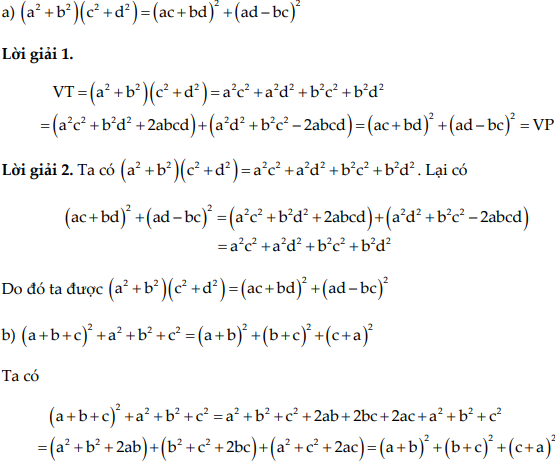
B. Lập phương của một tổng hoặc một hiệu

Dạng 1: Sử dụng hằng đẳng thức để khai triển và rút gọn biểu thức và tính giá trị biểu thức:  

a. Phương pháp giải:

Sử dụng hằng đẳng thức đã học để khai triển và rút gọn biểu thức.

b. Ví dụ minh họa:

VD1: Thực hiện phép tính:

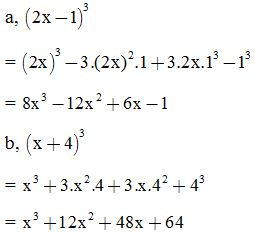
VD2: Rút gọn biểu thức:

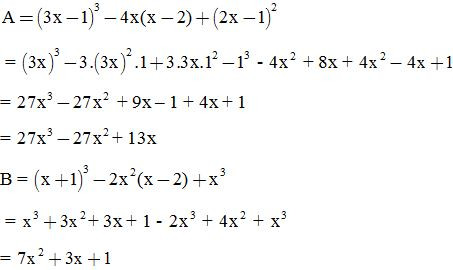
VD3: Viết các biểu thức sau dưới dạng lập phương một tổng hoặc lập phương một hiệu:

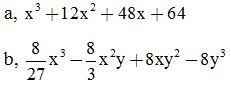
Giải:

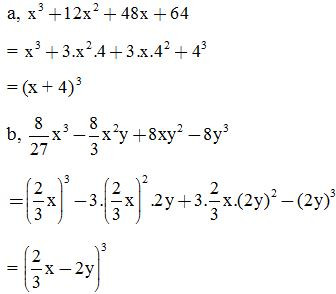
VD4: Tính giá trị các biểu thức sau:

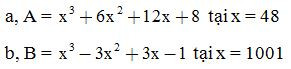
Giải:

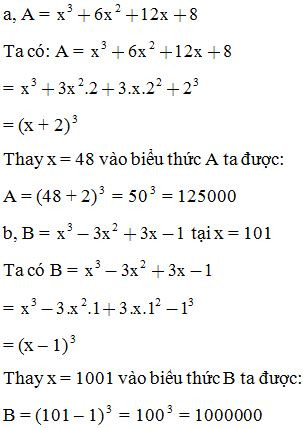
 Dạng 2: Sử dụng hằng đẳng thức để tính nhanh:

a. Phương pháp giải:

Sử dụng linh hoạt các hằng đẳng thức để tính nhanh

b. Ví dụ minh họa:

Tính nhanh:

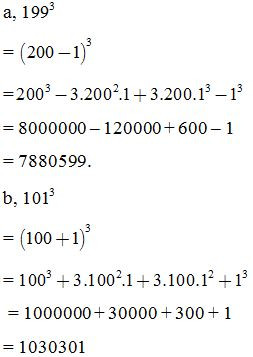
C. Tổng hoặc hiệu hai lập phương

1. Dạng 1: Sử dụng hằng đẳng thức để rút gọn và khai triển biểu thức:

a. Phương pháp giải:

Sử dụng các hằng đẳng thức đã học để khai triển hoặc rút gọn biểu thức.

b. Ví dụ minh họa:

VD1: Thực hiện phép tính:

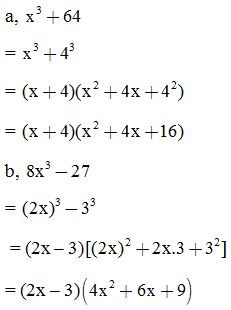
VD2: Rút gọn biểu thức:

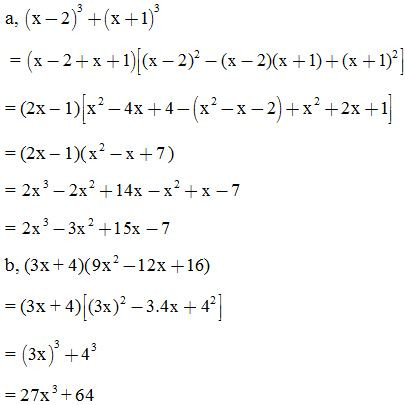
2. Dạng 2: Sử dụng hằng đẳng thức để tính nhanh

a, Phương pháp giải:

Sử dụng các hằng đẳng thức đã học để phân tích và tính

Chú ý thêm:

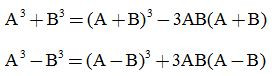
b, Ví dụ minh họa:

Tính nhanh:

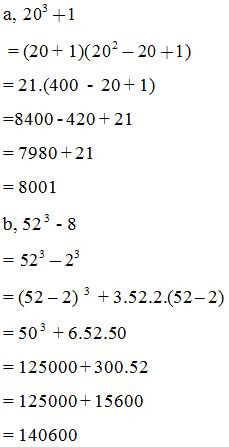
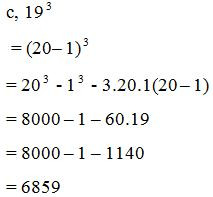
 Bài tập tự luyện

Bài 1: Thực hiện phép tính:

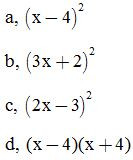
ĐS:

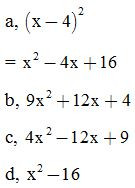
Bài 2: Thực hiện phép tính:

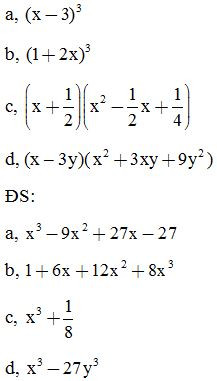
Bài 3: Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:

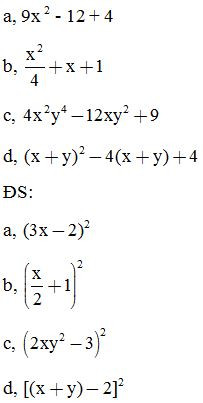
Bài 4: Chứng minh các đẳng thức sau:

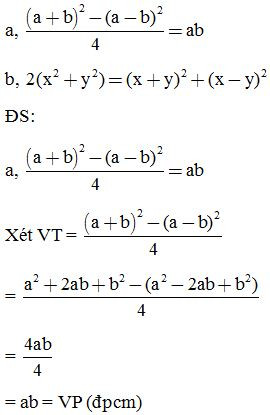
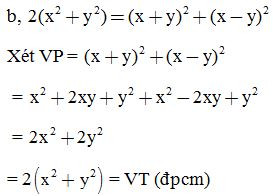
Bài 5: Rút gọn biểu thức:

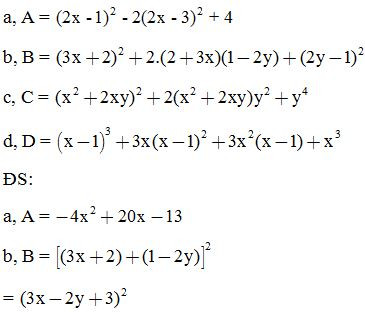
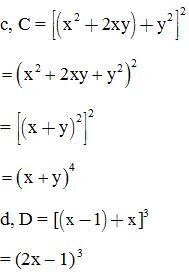
Bài 6: Rút gọn biểu thức:

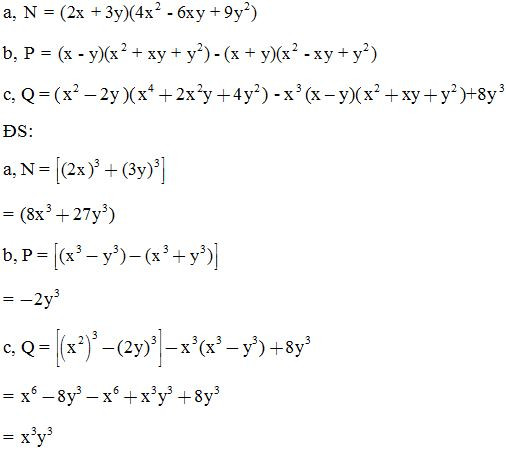
Bài 7: Tính giá trị của các biểu thức sau:

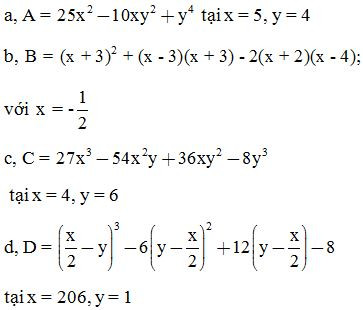
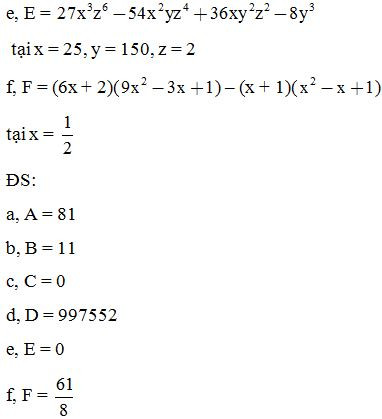
Bài 8: Tính nhanh:

a, 29²

b, 62.58

c, 102²

d, 101³

e, 91³  + 3.91² .9 + 3.91.9² + 9³

f, 18³ - 3.18² .8 + 3.18.8² - 2

g, 18³+2³

h, 23³ - 27

ĐS:

a, 29²

= (30 – 1)²

= 841

b, 62.58

= (60 + 2)(60 – 2)

= 60² - 2²

= 3596

c, 102²

= (100 + 2)²

= 10404

d, 101³

= (100 + 1)³

= 1030301

e, 91³ + 3.91² .9 + 3.91.9² + 9³

= (91 + 9)³

= 100³

= 1000000

f, 18³ - 3.18² .8 + 3.18.8² - 2⁹

 = (18 – 8)³

= 10³

= 1000

g, 18³ + 2³

= (18 + 2)³ – 3.18.2(18 + 2)

= 20³ - 6.18.20

= 5840

h, 23³ - 27

= 23³ - 3³

= (23 – 3)³ + 3.23.3.(23 – 3)

= 20³ + 9.23.20

= 12140

Bài 9: Tính giá trị biểu thức:

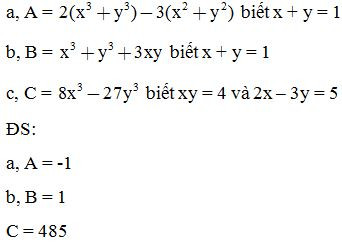
Bài 10: Chứng minh các biểu thức sau không phụ thuộc vào giá trị của biến x:

a, A =3(x – 1)² - (x + 1)² + 2(x – 3)(x + 3) – (2x + 3)² - (5 – 20x)

b, B = -x(x + 2)² + (2x + 1)² + (x + 3)(x² - 3x + 9) – 1

ĐS:

a, A = - 30

b, B = 27

Bài 11: Tính giá trị nhỏ nhất của biểu thức:

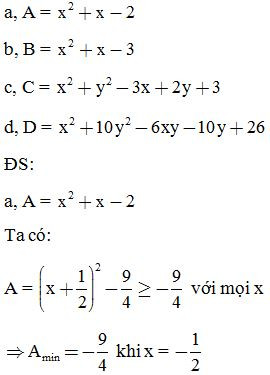
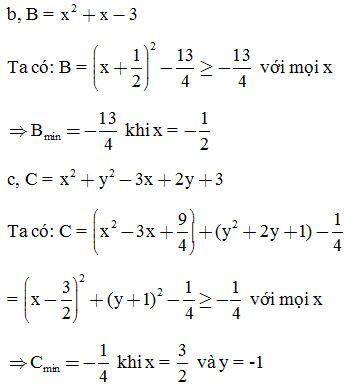
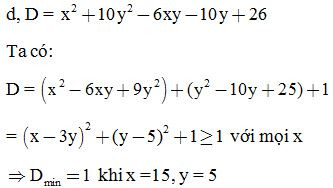
Bài 12: Tìm giá trị lớn nhất của biểu thức:

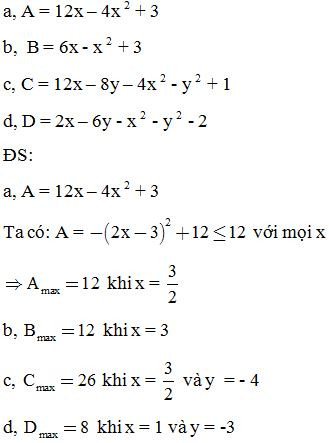
Bài 13: Chứng minh rằng với mọi a, b, c ta luôn có:

(a + b + c)³ = a³ + b³ + c³ + 3(a + b)(b + c)(c + a)

ĐS: Hướng dẫn:

Đặt a + b = A, B = c

Ta có: VT = (a + b + c)³

= (A + B)³ = A³ + B + 3A²B + 3AB²

Thay vào ta được:

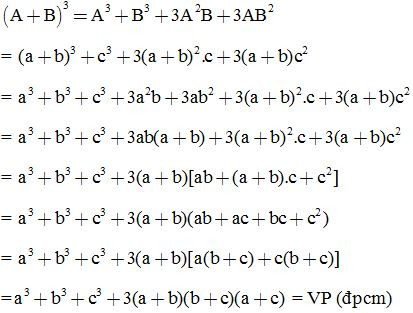
Bài 14: Biến đổi các biểu thức sau bằng việc áp dụng các hằng đẳng thức

a, (x + 2y)2

b, (x – 3y)(x + 3y)

c, (5 – x)2

d, (x – 1)2

e, (3 – y)2

f, (x – 1/2)2

Trả lời:

a, (x + 2y)2 = x2 + 4xy + 4y2

b, (x – 3y)(x + 3y) = x2 – (3y)2 = x2 – 9y2

c, (5 – x)2 = 52 – 10x + x2 = 25 – 10x + x2

d, (x – 1)2 = x2 – 2x + 1

e, (3 – y)2 = 9 – 6y + y2

f, (x – 1/2)2 = x2 – x + 1/4

Bài 15: Rút gọn biểu thức:

a, (x + y)2 + (x – y)2

b, 2(x – y)(x + y) + (x + y)2 + (x – y)2

c, (x – y + z)2 + (z – y)2 + 2(x – y + z)(y – z)

Trả lời:

a, (x + y)2 + (x – y)2

= x2 + 2xy + y2 + x2 – 2xy + y2

= 2x2 + 2y2

b, 2(x – y)(x + y) + (x + y)2 + (x – y)2

= [(x + y) + (x – y)]2 = (2x)2 = 4x2

c, (x – y + z)2 + (z – y)2 + 2(x – y + z)(y – z)

= (x – y + z)2 + 2(x – y + z)(y – z) + (y – z)2

= [(x – y + z) + (y – z)]2 = x2

Bài16: Tính giá trị của các biểu thức sau trên cơ sở áp dụng các hằng đẳng thức đã học

a, x2 – y2 tại x = 87 và y = 13

b, x3 + 9x2+ 27x + 27 tại x = 97

Trả lời:

a, Ta có: x2 – y2 = (x + y)(x – y)

Thay x = 87, y = 13, ta được:

x2 – y2 = (x + y)(x – y)

= (87 + 13)(87 – 13)

= 100.74 = 7400

b, Ta có: x3 + 9x2 + 27x + 27

= x3 + 3.x2.3 + 3.x.32 + 33

= (x + 3)3

Thay x = 97, ta được: (x + 3)3 = (97 + 3)3 = 1003 = 1000000

Bài 17: Chứng minh rằng:

(a + b)(a2 – ab + b2) + (a – b)(a2 + ab + b2) = 2a3

Trả lời:

 Ta có: (a + b)(a2 – ab + b2) + (a – b)(a2 + ab + b2)

= a3 + b3 + a3 – b3 = 2a3

Như vậy, vế trái bằng vế phải nên đẳng thức được chứng minh.

Bài 18: Áp dụng kiến thức về hằng đẳng thức để chứng tỏ rằng 4x – x2 – 5 < 0 với mọi x

Trả lời: Ta có: 4x – x2 – 5 = -(x2 – 4x + 4) – 1 = -(x – 2)2 -1

Vì (x – 2)2 ≥ 0 với mọi x nên –( x – 2)2 ≤ 0 với mọi x.

Suy ra: -(x – 2)2 - 1 ≤ 0 với mọi x

Vậy 4x – x2 – 5 < 0 với mọi x.

Bài 19: Áp dụng kiến thức về hằng đẳng thức hãy tìm giá trị nhỏ nhất của đa thức M = x2 + y2 – x + 6y + 10

Trả lời:  

Ta có: M = x2 + y2 – x + 6y + 10 = (y2 + 6y + 9) + (x2 – x + 1)

= (y + 3)2 + (x2 – 2.1/2 x + 1/4 + 3/4) = (y + 3)2 + (x – 1/2)2 + 3/4

Vì (y + 3)2 ≥ 0 và (x – 1/2)2 ≥ 0 nên (y + 3)2 + (x – 1/2)2 ≥ 0

⇒ (y + 3)2 + (x – 12)2 + 3/4 ≥ 3/4

⇒ M = 3/4 là giá trị nhỏ nhất khi (y + 3)2 =0

⇒ y = -3 và (x – 1/2)2 = 0 ⇒ x = 1/2

Vậy M = 3/4 là giá trị nhỏ nhất tại y = -3 và x = 1/2

Xem thêm các dạng bài tập hay, có đáp án:

70 Bài tập về những hằng đẳng thức đáng nhớ (có đáp án năm 2024) - Toán 8

20 Bài tập hằng đẳng thức đáng nhớ lớp 8 (2024) chi tiết nhất

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức (có đáp án năm 2024) - Toán 8

70 Bài tập về Giải bài toán bằng cách lập phương trình (có đáp án năm 2024) - Toán 8

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2024) - Toán 9