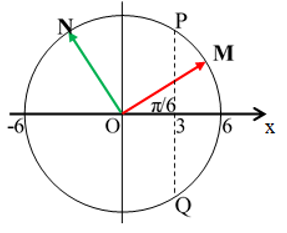
Trước tiên ta biểu diễn phương trình (1) trên vòng tròn, với φ = π/6 rad.
Vật xuất phát từ M, theo chiều âm.
a) Trong khoảng thời gian Δt = 2,5s
⇒ góc quét Δφ = Δt.ω = 2,5.5π = 12,5π = 6.2π + π/2
Từ vòng tròn ta thấy:
Trong một chu kỳ vật qua x = 3 cm được 2 lần tại P (chiều âm) và Q (chiều dương)
Trong Δφ1 = 6.2π ; 6 chu kỳ vật qua x = 3 cm được 6.2 = 12 lần
Còn lại Δφ2 = π/2 từ M → N vật qua x = 3 cm một lần tại P (chiều âm).
Vậy: Trong khoảng thời gian Δt = 2,5 s vật qua x = 3 cm được 12 + 1 = 13 lần.
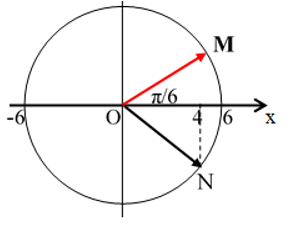
b. Trong khoảng thời gian Δt = 2 s
⇒ góc quét Δφ = Δt.ω = 2.5π = 10π = 5.2π
Vật thực hiện được 5 chu kỳ (quay được 5 vòng)
Từ vòng tròn ta thấy:
Trong một chu kỳ vật qua vị trí x = +4 cm theo chiều dương được một lần (tại N)
Vậy: trong 5 chu kỳ thì vật qua vị trí x = 4 cm theo chiều dương được 5 lần.
c. Trong khoảng thời gian Δt = 2,5s
⇒ góc quét Δφ = Δt.ω = 2,5.5π = 12,5π = 6.2π + π/2
Từ vòng tròn ta thấy:
Trong một chu kỳ vật qua vị trí cân bằng theo chiều dương 1 lần tại P.
Trong Δφ1 = 6.2π ; 6 chu kỳ vật qua vị trí cân bằng theo chiều dương 6 lần tại P.
Còn lại Δφ2 = π/2 từ M → N vật qua không qua vị trí cân bằng theo chiều dương lần nào. Vậy trong khoảng thời gian Δt = 2,5s vật qua vị trí cân bằng theo chiều dương 6 lần.
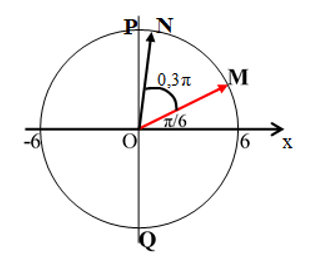
d) Trong khoảng thời gian Δt = 2,86s
⇒ góc quét Δφ = Δt.ω = 2,86.5π = 14,3π = 7.2π + 0,3π
Từ vòng tròn ta thấy:
Trong một chu kỳ vật qua vị trí cân bằng 2 lần tại P(chiều âm) và Q(chiều dương).
Trong Δφ1 = 7.2π; 7 chu kỳ vật qua vị trí cân bằng 14 lần tại P và Q.
Còn lại Δφ2 = 0,3π từ M → N vật qua không qua vị trí cân bằng lần nào.
Vậy trong khoảng thời gian Δt = 2,86s vật qua vị trí cân bằng 15 lần.