Trong đồ thị có trọng số ở Hình 15, mỗi cạnh biểu diễn một tuyến xe buýt giữa hai bến trong các bến xe A, B, C, D, E và F, trọng số của mỗi cạnh biểu diễn thời gian tính bằng giờ của tuyến xe buýt tương ứng. Một người cần ít nhất bao nhiêu thời gian để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên? Biết rằng thời gian tại bến để chuyển tiếp từ tuyến này qua tuyến kia là không đáng kể.

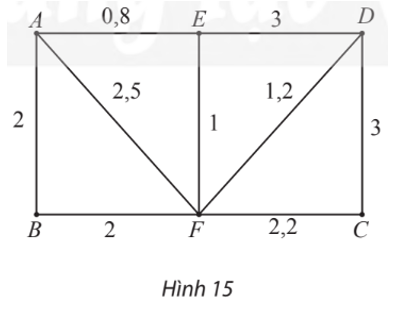
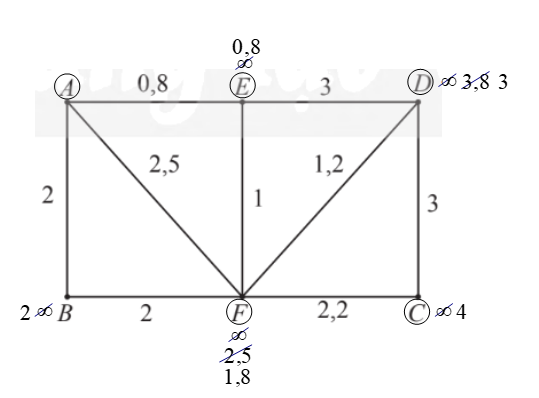
Ta tìm khoảng thời gian ít nhất để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên bằng cách sử dụng thuật toán Dijkstra như sau:

– Gán nhãn cho A bằng 0 (tức là, n_A = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.

– Tại các đỉnh kề với đỉnh A, gồm E, F, B, ta có:

⦁ n_E = n_A + w_AE = 0 + 0,8 = 0,8. Vì 0,8 < ∞ nên ta đổi nhãn của E thành 0,8.

⦁ n_F = n_A + w_AF = 0 + 2,5 = 2,5. Vì 2,5 < ∞ nên ta đổi nhãn của F thành 2,5.

⦁ n_B = n_A + w_AB = 0 + 2 = 2. Vì 2 < ∞ nên ta đổi nhãn của B thành 2.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần đỉnh A nhất, chỉ tính các đỉnh khác đỉnh A).

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E gồm D, F, ta có:

⦁ n_D = n_E + w_DE = 0,8 + 3 = 3,8. Vì 3,8 < ∞ nên ta đổi nhãn của D thành 3,8.

⦁ n_F = n_E + w_EF = 0,8 + 1 = 1,8. Vì 1,8 < 2,5 (2,5 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 1,8.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ hai).

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F gồm B, C, D, ta có:

⦁ n_B = n_F + w_FB = 1,8 + 2 = 3,8. Vì 3,8 > 2 (2 là nhãn hiện tại của B) nên ta giữ nguyên nhãn của B là 2.

⦁ n_C = n_F + w_FC = 1,8 + 2,2 = 4. Vì 4 < ∞ nên ta đổi nhãn của C thành 4.

⦁ n_D = n_F + w_FD = 1,8 + 1,2 = 3. Vì 3 < 3,8 (3,8 là nhãn hiện tại của D) nên ta đổi nhãn của D thành 3.

Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B. Nhưng do trong các đỉnh chưa được khoanh tròn còn lại, ta thấy không có đỉnh nào kề với đỉnh B nên ta chọn lại đỉnh có nhãn bé nhất (ngoại trừ đỉnh B) là đỉnh D (đỉnh gần A thứ ba).

– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ còn đỉnh C, ta có:

n_C = n_D + w_DC = 3 + 3 = 6. Vì 6 > 4 (4 là nhãn hiện tại của C) nên ta giữ nguyên nhãn của C là 4.

Lúc này, ngoại trừ đỉnh B, ta thấy chỉ còn đỉnh C chưa được khoanh tròn nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).

– Nhìn ngược lại các bước trên, ta thấy:

n_C = 4 = n_F + w_FC

= n_E + w_EF + w_FC

= n_A + w_AE + w_EF + w_FC

= w_AE + w_EF + w_FC

= l_AEFC.

Vậy người đó cần ít nhất 4 giờ để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên.