Tìm x, y là số nguyên, biết: a) x.y = 11

Đề bài: Tìm x, y là số nguyên, biết:

a) x.y = 11;

b) (2x + 1)(3y – 2) = 12;

c) 1 + 2 + 3 + … + x = 55;

d) 6 ⋮ (x – 1);

e) (2x + 1)³ = 27;

f) 2^x.16 = 128.

Trả lời

Hướng dẫn giải:

a) x.y = 11 = 1.11.

$\Rightarrow \left\{\begin{array}{l}x=1\\ y=11\end{array}\right.$ hoặc $\left\{\begin{array}{l}x=11\\ y=1\end{array}\right.$

Vậy (x; y) ∈ {(1; 11), (11; 1)}.

b) (2x + 1)(3y – 2) = 12

Ta có {2x + 1; 3y – 2} ∈ Ư(12).

Ư(12) ∈ {1; 2; 3; 4; 6; 12}.

Ta có bảng sau:

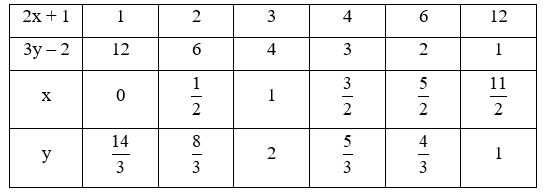
Mà x, y là số nguyên nên $\left(x;y\right)=\left(1;2\right)$

Vậy $\left(x;y\right)=\left(1;2\right)$ .

c) Từ 1 đến x có: (x – 1) : 1 + 1 = x số hạng.

Ta có 1 + 2 + 3 + … + x = 55

⇔ (x + 1) . x : 2 = 55

⇔ (x + 1) . x = 110

⇔ x² + x – 110 = 0

⇔ x² – 10x + 11x – 110 = 0

⇔ x(x – 10) + 11(x – 10) = 0

⇔ (x – 10)(x + 11) = 0

⇔ x – 10 = 0 hoặc x + 11 = 0

⇔ x = 10 hoặc x = –11.

Vậy x ∈ {10; –11}.

d) Ta có 6 chia hết cho (x – 1).

Suy ra x – 1 ∈ {1; 2; 3; 6}.

Vậy x ∈ {2; 3; 4; 7}.

e) (2x + 1)³ = 27

⇔ (2x + 1)³ = 3³

⇔ 2x + 1 = 3

⇔ 2x = 2

⇔ x = 1.

Vậy x ∈ {1}.

f) 2^x.16 = 128

⇔ 2^x = 8

⇔ 2^x = 2³

⇔ x = 3.

Vậy x ∈ {3}.