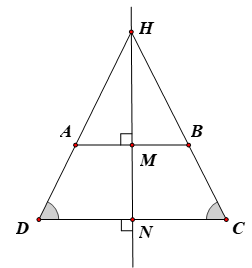
Gọi H là giao điểm của AD và BC.

Ta có $\widehat{ADC}=\widehat{BCD}$ (do ABCD là hình thang cân).

Suy ra tam giác HCD cân tại H.

Do đó HD = HC.

Vì vậy HD – AD = HC – BC (AD = BC vì ABCD là hình thang cân có hai đáy AB, CD).

Suy ra HA = HB.

Do đó tam giác HAB cân tại H.

Gọi M, N lần lượt là trung điểm của AB và CD.

Tam giác HCD cân tại H có HN là đường trung tuyến.

Suy ra HN cũng là đường cao của tam giác HCD, do đó HN ⊥ CD.

Chứng minh tương tự, ta được HM ⊥ AB.

Mà AB // CD (chứng minh trên).

Suy ra HM ⊥ CD

Lại có HN ⊥ CD (chứng minh trên).

Do đó ba điểm H, M, N thẳng hàng.

Ta có M là trung điểm AB và MN ⊥ AB (chứng minh trên).

Suy ra MN là đường trung trực của hai đoạn thẳng AB.

Khi đó B = Đ_MN(A) và A = Đ_MN(B).

Chứng minh tương tự, ta được D = Đ_MN(C) và C = Đ_MN(D).

Do đó ảnh của hình thang cân ABCD qua Đ_MN là chính nó.

Vậy trục đối xứng cần tìm là đường thẳng MN, với M, N lần lượt là trung điểm của AB và CD.