Thể tích khối tứ diện đều cạnh 3 căn bậc hai của 2 bằng A. 9 B. 3 căn bậc hai của 2 C. 6 D. 3 căn bậc hai của 2
Thể tích khối tứ diện đều cạnh \(3\sqrt 2 \) bằng
A. \(9\).
B. \(3\sqrt 2 \).
C. \(6\).
D. \(3\sqrt 2 \).
Lời giải
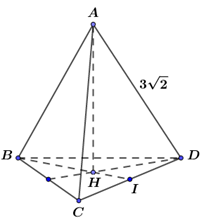
Cách 1: Ta tính thể tích khối tứ diện đều \[ABCD\] có cạnh bằng \(3\sqrt 2 \).
Ta có \({S_{\Delta BCD}} = \frac{1}{2}.3\sqrt 2 .3\sqrt 2 .\sin 60^\circ = \frac{{9\sqrt 3 }}{2}\,\,.\) Gọi \[H\] là trọng tâm \(\Delta BCD \Rightarrow AH \bot \left( {BCD} \right)\,\,.\)
Gọi \[I\] là trung điểm \[CD\]\[ \Rightarrow \,BI = \frac{{3\sqrt 6 }}{2} \Rightarrow \,BH = \frac{2}{3}BI = \sqrt 6 \,\,\,.\]
\[ \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{{\left( {3\sqrt 2 } \right)}^2} - {{\sqrt 6 }^2}} = 2\sqrt 3 \,\,\,.\]
Thể tích khối tứ diện đều cạnh \(3\sqrt 2 \) bằng: \({V_{ABCD}} = \frac{1}{3}.AH.{S_{\Delta BCD}} = \frac{1}{3}.2\sqrt 3 .\frac{{9\sqrt 3 }}{2} = 9\,\,.\)
Cách 2: Thể tích khối tứ diện đều có cạnh bằng \(a\)là \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
Cách 2: Thể tích khối tứ diện đều có cạnh bằng \(a\)là \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
Suy ra thể tích khối tứ diện đều có cạnh bằng \(3\sqrt 2 \) là \(\frac{{{{\left( {3\sqrt 2 } \right)}^3}\sqrt 2 }}{{12}} = 9\,\,.\)