Một vụ nổ được hai micro M₁ và M₂ cách nhau 2 dặm ghi lại (1 dặm bằng 5 280 feet). Micro M₁ nhận được âm thanh trước 4 giây so với micro M₂. Giả sử âm thanh di chuyển với tốc độ 1 100 feet/giây. Tập tất cả các điểm P xảy ra vụ nổ thỏa mãn các điều kiện trên là một hypebol có phương trình dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, với hai micro M₁ và M₂ là các tiêu điểm. Khi đó a + b bằng bao nhiêu? (làm tròn đến chữ số hàng đơn vị)

A. 2 200;

B. 4 800;

Hướng dẫn giải:

Đáp án đúng là: D

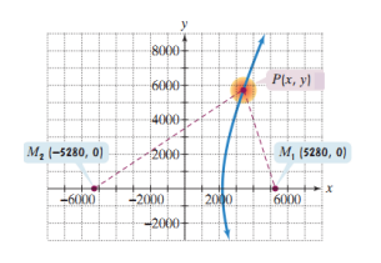
Ta bắt đầu bằng cách đặt micro trong một hệ tọa độ vuông góc. Bởi vì  dặm bằng 5 280 feet nên ta đặt M₁ trên trục hoành cách gốc tọa độ 5280 feet về bên phải và đặt M₂ trên trục hoành cách gốc tọa độ 5 280 feet về bên trái như hình vẽ minh họa hai micro cách nhau 2 dặm.

Ta biết rằng M₂ nhận được âm thanh sau 4 giây so với M₁. Vì âm thanh di chuyển với tốc độ 1 100 feet/giây nên hiệu số khoảng cách từ P (nơi xảy ra vụ nổ) tới M₂ và từ P tới M₁ là 4 400 feet.

Tập tất cả các điểm P xảy ra vụ nổ thỏa mãn các điều kiện này là một hyperbol, với hai micro M₁ và M₂ là các tiêu điểm.

Như vậy, vị trí xảy ra vụ nổ nằm trên hyperbol có phương trình chuẩn là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$.

Ta cần xác định các hệ số a và b.

Ta có hiệu số khoảng cách giữa hai micro là 4 400 feet và được đặt bằng 2a, tức là 2a = 4 400 suy ra a = 2 200.

Ta có $\frac{x^2}{2{200}^2}-\frac{y^2}{b^2}=1$ hay $\frac{x^2}{4840000}-\frac{y^2}{b^2}=1$.

Ta lại có khoảng cách từ gốc O(0; 0) tới tiêu điểm M₂(–5 280; 0) hoặc M₁(5 280; 0) đều bằng 5 280. Do đó c = 5 280.

Sử dụng hệ thức $c^2=a^2+b^2\Rightarrow b=\sqrt{5{280}^2-2{200}^2}\approx 4800.$

Vậy a + b = 2 200 + 4 800 = 7 000.