Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao
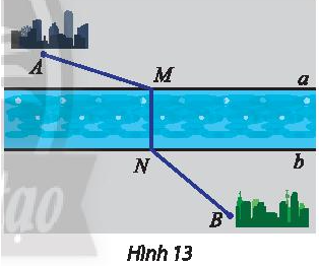
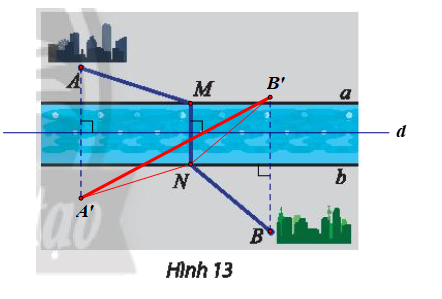
Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.