Lời giải

Chọn A

Phương trình hoành độ giao điểm \( - {x^4} + {x^2} + 4x - 2 = {x^2} + \left( {{m^2} + m} \right)x + 1 \Leftrightarrow - {x^4} + 4x - 3 = \left( {{m^2} + m} \right)x\)

Do \(x = 0\)không thỏa mãn phương trình (1) nên ta có \({m^2} + m = - {x^3} + 4 - \frac{3}{x} = f\left( x \right)\) (1)

Ta có \(f'\left( x \right) =  - 3{x^2} + \frac{3}{{{x^2}}} = \frac{{ - 3\left( {{x^4} - 1} \right)}}{{{x^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 1}\end{array}} \right.\). Ta có bảng biến thiên

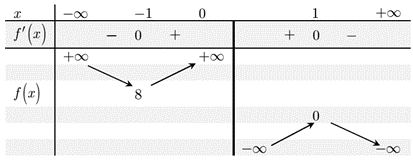
Dựa vào bảng biến thiên để \(\left( P \right)\)cắt \(\left( C \right)\)tại hai điểm phân biệt thì (1) có 2 nghiệm phân biệt

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{m^2} + 2m > 8}\\{{m^2} + 2m < 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m < - 4}\\{m > 2}\\{ - 2 < m < 0}\end{array}} \right.\).

Do \(m\)nguyên và thuộc \(\left( { - 2019;2020} \right)\)nên \(m\)nhận các giá trị sau \(m \in \left\{ { - 2018; - 2017;.., - 6; - 5} \right\}\), \(m \in \left\{ {3;4;..;2019} \right\}\)và \(m = - 1\).

Vậy có tất cả \(4032\)giá trị \(m\).