Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC. a) Chứng minh EK // CD, FK // AB. b) So sánh EF và
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
b) So sánh EF và
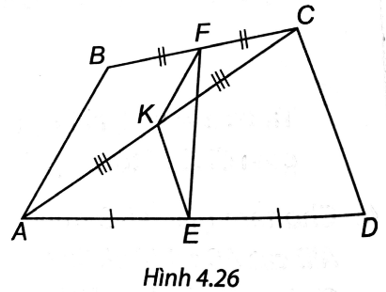
a) ∆ABC có F là trung điểm BC, K là trung điểm AC nên FK là đường trung bình của ∆ABC, suy ra FK // AB.
∆ACD có E là trung điểm AD nên EK là đường trung bình của ∆ACD, suy ra EK // CD.
b) FK là đường trung bình của ∆ABC nên AB = 2FK.
Tương tự CD = 2EK.
Ta có FK + KE ≥ FE nên ≥ EF.
Do đó EF ≤