Cho tứ diện ABCD. Trên các cạnh AC, CD lần lượt lấy các điểm E, F sao cho CE = 3EA, DF = 2FC. a) Xác định giao tuyến của mặt phẳng (BEF) với các mặt phẳng (ABC), (ACD), (BCD). b) Xác định g
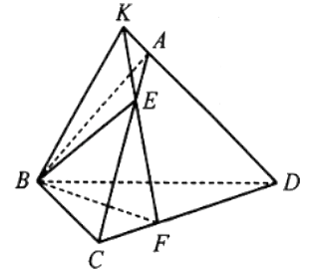
Cho tứ diện ABCD. Trên các cạnh AC, CD lần lượt lấy các điểm E, F sao cho CE = 3EA, DF = 2FC.
a) Xác định giao tuyến của mặt phẳng (BEF) với các mặt phẳng (ABC), (ACD), (BCD).
b) Xác định giao điểm K của đường thẳng AD với mặt phẳng (BEF).
c) Xác định giao tuyến của hai mặt phẳng (BEF) và (ABD).