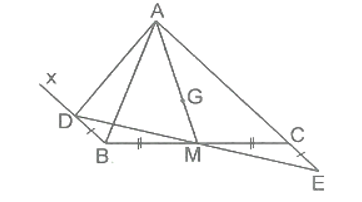
Cho tam giác ABC. Vẽ tia Bx song song AC (sao cho góc xBA và góc BAC là một cặp góc so le trong).
5
16/11/2024
Cho tam giác ABC. Vẽ tia Bx // AC (sao cho và là một cặp góc so le trong).Lấy điểm D ∈ Bx và điểm E thuộc tia đối của tia CA sao cho BD = CE. Hai tam giác nào sau đây có cùng trọng tâm?
C. ΔAME và ΔABE;
D. ΔABC và ΔADE.
Trả lời
Hướng dẫn giải:
Đáp án đúng là: D
Gọi M là trung điểm của BC. Suy ra MB = MC.
Xét ΔBMD và ΔCME có:
BD = CE (giả thiết);
(cặp góc so le trong của Bx // AC);
MB = MC
Do đó ΔBMD = ΔCME (c.g.c).
Suy ra MD = ME (hai cạnh tương ứng) và (hai góc tương ứng)
Ta có (kề bù).
Do đó suy ra D, M, E thẳng hàng.
Ta có ba điểm D, M, E thẳng hàng và MD = ME nên M là trung điểm của DE.
Khi đó ΔABC và ΔADE chung đỉnh A, chung đường trung tuyến AM nên trọng tâm G của hai tam giác này trùng nhau.