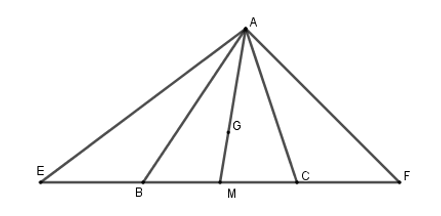
Cho tam giác ABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF
4
16/11/2024
Cho ΔABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF. Gọi G là trọng tâm tam giác ABC. Tia AG cắt BC tại M. Khẳng định nào sau đây là đúng?
A. Hai tam giác ABC và AEF có cùng trọng tâm;
B. Hai tam giác ABC và AEC có cùng trọng tâm;
C. Hai tam giác ABC và ABF có cùng trọng tâm;
D. Hai tam giác AEM và AMF có cùng trọng tâm.
Trả lời
Hướng dẫn giải:
Đáp án đúng là: A
Ta có: G là trọng tâm của tam giác ABC nên AG là trung tuyến của tam giác
Mà AG cắt BC tại M nên M là trung điểm của BC
Do đó MB = MC.
Lại có BE = CF (giả thiết)
Nên MB + BE = MC + CF hay ME = MF.
Suy ra AM là đường trung tuyến ứng với cạnh EF của ΔAEF.
Mặt khác (do G là trọng tâm của ΔABC).
Do đó G là trọng tâm của ΔAEF
Mà G là trọng tâm của ΔABC, nên hai tam giác ABC và AEF có cùng trọng tâm là điểm G.
Vậy ta chọn phương án A.