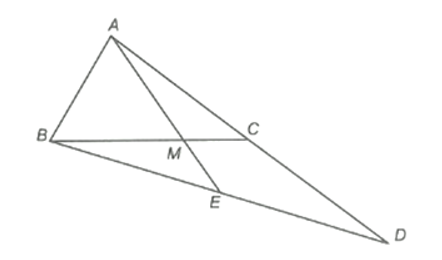
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm
Cho ∆ABC, điểm M thuộc cạnh BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là
A. Trọng tâm của ΔABD;
B. Trọng tâm của ΔABC;
C. Trọng tâm của ΔABE;
D. Cách đều ba đỉnh của ΔABD.