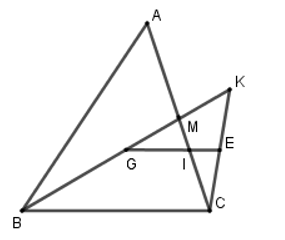
Cho tam giác ABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho BG = 2/.3 BM

Cho ΔABC có đường trung tuyến BM. Trên tia BM lấy hai điểm G, K sao cho $BG=\frac{2}{3}BM$ và G là trung điểm của BK. Gọi E là trung điểm CK; GE cắt AC tại I. Số thích hợp để điền vào chỗ trống CI = … AC là:

C. $\frac{1}{2};$

Trả lời