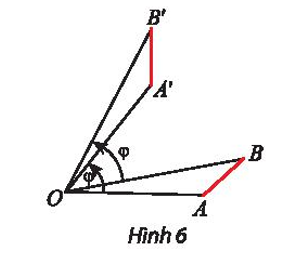
Cho phép quay Q_{(O; φ)} và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?

Ta có Q(O, φ) biến điểm A khác O thành điểm A’ sao cho OA = OA’ và (OA, OA’) = φ nên $\widehat{AO{A}^{\text{'}}}=\phi$.

Tương tự, ta có Q(O, φ) biến điểm B khác O thành điểm B’ sao cho OB = OB’ và (OB, OB’) = φ nên $\widehat{BO{B}^{\text{'}}}=\phi$.

Ta có $\widehat{AO{A}^{\text{'}}}=\widehat{BO{B}^{\text{'}}}\left(=\phi \right)$.

Suy ra $\widehat{AOB}+\widehat{BO{A}^{\text{'}}}=\widehat{BO{A}^{\text{'}}}+\widehat{A^{\text{'}}O{B}^{\text{'}}}$.

Do đó $\widehat{AOB}=\widehat{A^{\text{'}}O{B}^{\text{'}}}$.

Xét ∆OAB và ∆OA’B’, có:

OA = OA’ (chứng minh trên);

OB = OB’ (chứng minh trên);

$\widehat{AOB}=\widehat{A^{\text{'}}O{B}^{\text{'}}}$ (chứng minh trên).

Vậy ∆OAB = ∆OA’B’ (c.g.c).