Lời giải:
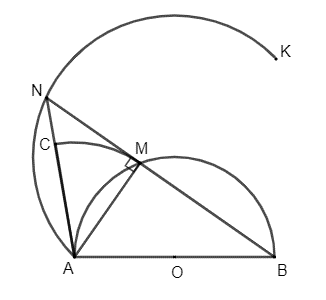
Trên cạnh AN, lấy điểm C sao cho AC = AM.
Tam giác AMN vuông cân tại M nên \(\widehat {CAM} = \widehat {NAM} = 45^\circ \) và AN = \(\sqrt 2 \)AM = \(\sqrt 2 \)AC.
Vì AM = AC và \(\widehat {CAM} = 45^\circ \) nên ta có phép quay tâm A, góc quay 45° biến điểm M thành điểm C.
Vì AN = \(\sqrt 2 \)AC và C thuộc AN nên \(\overrightarrow {AN} = \sqrt 2 \overrightarrow {AC} \), do đó ta có phép vị tự tâm A, tỉ số \(\sqrt 2 \) biến điểm C thành điểm N.
Như vậy, phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm A, góc quay 45° và phép vị tự tâm A, tỉ số \(\sqrt 2 \) biến điểm M thành điểm N. Mặt khác, M thuộc nửa đường tròn đường kính AB nên N thuộc nửa đường tròn đường kính AK cố định là ảnh của nửa đường tròn đường kính AB qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm A, góc quay 45° và phép vị tự tâm A, tỉ số \(\sqrt 2 \). Ở đó K là ảnh của B qua phép đồng dạng trên, K thỏa mãn \(\widehat {BAK} = 45^\circ \) (theo chiều dương) và AK = \(\sqrt 2 \)AB.