Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng ( AB'C') tạo với mặt đáy góc 60^0. Tính theo a thể tích lăng trụ ABC.A'B'C'
38
27/04/2024
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Mặt phẳng \(\left( {AB'C'} \right)\) tạo với mặt đáy góc \(60^\circ \). Tính theo \(a\) thể tích lăng trụ \(ABC.A'B'C'\).
A. \(\frac{{3{a^3}\sqrt 3 }}{8}\).
B. \(\frac{{3{a^3}\sqrt 3 }}{4}\).
C. \(\frac{{{a^3}\sqrt 3 }}{8}\).
D. \(\frac{{{a^3}\sqrt 3 }}{2}\).
Trả lời
Lời giải
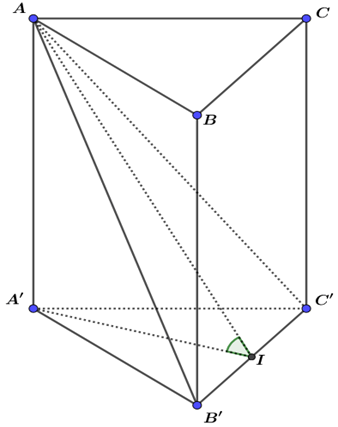
Gọi \[I\] là trung điểm của \[B'C' \Rightarrow A'I \bot B'C'\] và \[A'I = \frac{{a\sqrt 3 }}{2}\], do \[AA' \bot \left( {A'B'C'} \right) \Rightarrow AA' \bot B'C' \Rightarrow B'C' \bot \left( {AA'I} \right) \Rightarrow \left( {\left( {AB'C'} \right)\,;\,\left( {ABC} \right)} \right) = \widehat {{\rm{AIA'}}} = {60^^\circ }\].
\[ \Rightarrow AA' = A'I\tan {60^^\circ } = \frac{{3a}}{2}\].
\[{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4} \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\].

