Cho lăng trụ ABC.A'B'C', đáy là tam giác đều cạnh a, AA' = AB' = AC' = a. Thể tích khối lăng trụ đã cho bằng. A. a^3 căn bậc hai của 3 /4 B. a^3 căn bậc hai của 2/4 C. a^3 căn bậc hai
39
26/04/2024
Cho lăng trụ \(ABC.A'B'C'\), đáy là tam giác đều cạnh \(a,\) \[AA' = AB' = AC' = a.\] Thể tích khối lăng trụ đã cho bằng.
A. \(\frac{{{a^3}\sqrt 3 }}{4}\)
B. \(\frac{{{a^3}\sqrt 2 }}{4}\)
C. \(\frac{{{a^3}\sqrt 2 }}{6}\)
D. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
Trả lời
Lời giải
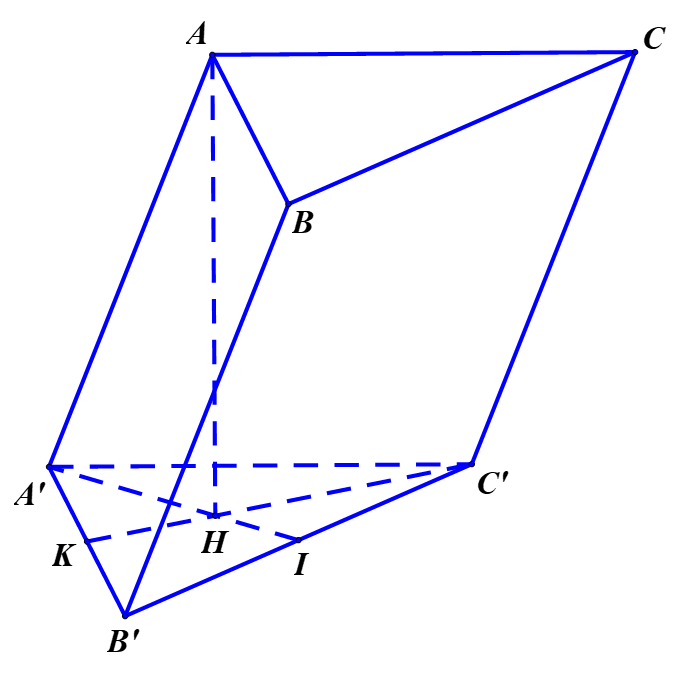
Chọn B.
Ta thấy \(A.A'B'C'\) là tứ diện đều cạnh \(a.\)
Mà \({V_{A.A'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}} \Rightarrow {V_{ABC.A'B'C'}} = 3{V_{A.A'B'C'}}\)
Gọi \(H\) là tâm của đường tròn ngoại tiếp tam giác \(A'B'C'\).
Thì \(AH\) là đường cao của hình chóp \(A.A'B'C'\).
Ta có \(A'H = \frac{{a\sqrt 3 }}{3}.\)
Tam giác \(AA'H\) vuông tại \(H\) nên :
\(A{H^2} = AA{'^2} - A'{H^2} = {a^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = {a^2} - \frac{{{a^2}}}{3} = \frac{{6{a^2}}}{9} \Rightarrow AH = \frac{{a\sqrt 6 }}{3}\) .
Diện tích tam giác \(A'B'C'\) là: \(S = \frac{{{a^2}\sqrt 3 }}{4}\) nên thể tích khối tứ diện \(AA'B'C'\) là:
\({V_{A.A'B'C'}} = \frac{1}{3}AH.S = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
Vậy thể tích khối lăng trụ là: \(V = 3.{V_{A.A'B'C'}} = \frac{{{a^3}\sqrt 2 }}{4}\) .

