Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng ( ABC') và ( A'B'C) chia khối lăng trụ thành 4 khối đa diện, kí hiệu (H1, H2) lần lượt là khối đa diện có thể tích lớn nhất và nhỏ nhấ
35
27/04/2024
Cho khối lăng trụ tam giác đều \(ABC.A'B'C'\). Các mặt phẳng \(\left( {ABC'} \right)\) và \(\left( {A'B'C} \right)\) chia khối lăng trụ thành 4 khối đa diện, kí hiệu \({H_1},{\rm{ }}{H_2}\) lần lượt là khối đa diện có thể tích lớn nhất và nhỏ nhất trong 4 khối đa diện. Gọi \({V_{\left( {{H_1}} \right)}},{\rm{ }}{V_{\left( {{H_2}} \right)}}\) lần lượt là thể tích của \[{H_1}\] và \[{H_2}\]. Tỉ số \(\frac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}}\) bằng
A. \(3\).
B. \(4\).
C. \(2\).
D. \(5\).
Trả lời
Lời giải
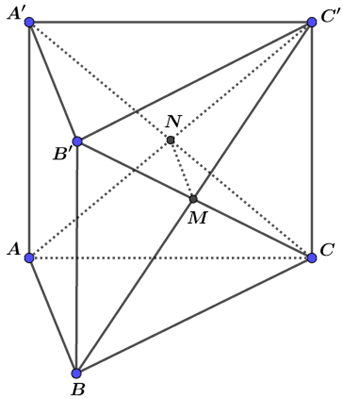
Gọi \[V\] là thể tích khối lăng trụ \[ABC.A'B'C'\] và \[\left\{ \begin{array}{l}M = BC' \cap B'C\\N = A'C \cap AC'\end{array} \right. \Rightarrow M\,,\,N\] lần lượt là trung điểm của \[BC'\,,\,AC'\].
+) Thể tích khối \[C'CMN\].
Ta có \[\left\{ \begin{array}{l}\frac{{{V_{C'CMN}}}}{{{V_{C'CAB}}}} = \frac{{C'N}}{{C'A}}.\frac{{C'M}}{{C'B}} = \frac{1}{4}\\{V_{C'CAB}} = \frac{1}{3}V\end{array} \right.
\Rightarrow {V_{C'CMN}} = \frac{1}{{12}}V\].
+) Thể tích khối \[MNCAB\]: \[{V_{MNCAB}} = {V_{C'CAB}} - {V_{C'CMN}} = \frac{1}{3}V - \frac{1}{{12}}V = \frac{1}{4}V\].
+ Thể tích khối \[MNC'A'B'\]: \[{V_{MNC'A'B'}} = {V_{CC'A'B'}} - {V_{C'CMN}} = \frac{1}{3}V - \frac{1}{{12}}V = \frac{1}{4}V\].
+) Thể tích khối \[MNABB'A'\]: \[{V_{MNABB'A'}} = V - \frac{1}{{12}}V - \frac{1}{4}V - \frac{1}{4}V = \frac{5}{{12}}V\].
Từ đó \[\frac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}} = \frac{{{V_{MNABB'A'}}}}{{{V_{C'CMN}}}} = 5\].

