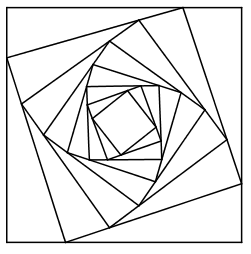
Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (Hình 4)
Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (Hình 4). Từ hình vuông C2 lại làm tiếp tục như trên để có hình vuông C3. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông C1, C2, C3, ..., Cn, ... Gọi an là độ dài cạnh hình vuông Cn. Chứng minh dãy số (an) là cấp số nhân.