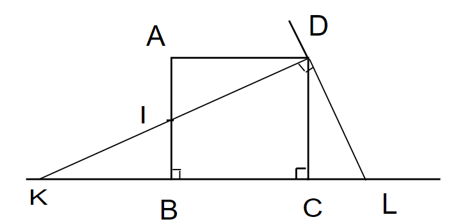
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng: Tổng $\frac{1}{D{I}^2}+\frac{1}{D{K}^2}$ không đổi khi I thay đổi trên cạnh AB.