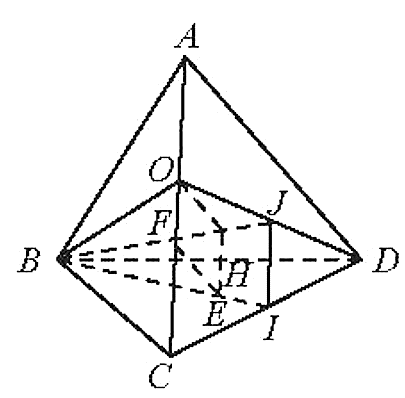
Gọi O là trung điểm AC, J là trung điểm OD.

Vě OH ^ BJ, HE // AC, EF // OH.

Có IJ // AC nên AC // (BIJ).

Þ d(AC, BI) = d(AC, (BIJ)) = d(O, (BIJ)).

Do ABCD là tứ diện đều nên ta dễ dàng nhận ra AC ^ (OBD).

Þ AC ^ OH (OH Ì OBD).

AC // IJ, Þ OH ^ IJ.

Kết hợp giả thiết, suy ra OH ^ (BIJ) hay d(O, (BIJ)) = OH.

Xét tam giác OBD cân tại O, ta có

$\begin{array}{l}BD=\sqrt{11}.\\ OB=OD=BD.\frac{\sqrt{3}}{2}=\frac{\sqrt{33}}{2}\\ \Rightarrow BJ=\frac{\sqrt{11}}{4}\end{array}$

Áp dụng công thức Heron, ta có:

 $S_{OBD}=\frac{11\sqrt{2}}{4}\Rightarrow S_{OBJ}=\frac{11\sqrt{2}}{4}.$

Ta tính được OH = $\sqrt{2}$

Vậy khoảng cách giữa hai đường thẳng AC và BI là $\sqrt{2}$