Lời giải

Chọn C

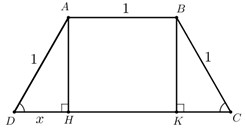
Kẻ \(AH \bot CD,BK \bot CD \Rightarrow ABKH\) là hình chữ nhật \( \Rightarrow AB = HK = 1\left( m \right).\)

Đặt \(DH = x.\) Khi đó \(AH = \sqrt {1 - {x^2}} \left( {0 < x < 1} \right).\)

Vì \(ABCD\) là hình thang cân nên \(\Delta ADH = \Delta BCK\) (cạnh huyền – góc nhọn)

  \( \Rightarrow DH = CK = x \Rightarrow CD = DH + HK + CK = 2x + 1.\)

Ta có \({S_{ABCD}} = \frac{{\left( {AB + CD} \right).AH}}{2} = \frac{{\left( {1 + 2x + 1} \right)\sqrt {1 - {x^2}} }}{2} = \left( {x + 1} \right)\sqrt {1 - {x^2}} .\)

Xét hàm số \(f\left( x \right) = \left( {x + 1} \right)\sqrt {1 - {x^2}} \left( {0 < x < 1} \right),\) ta có

\(f'\left( x \right) = \sqrt {1 - {x^2}} - \frac{{2x\left( {x + 1} \right)}}{{2\sqrt {1 - {x^2}} }} = \frac{{ - 2{x^2} - x + 1}}{{\sqrt {1 - {x^2}} }},\) \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{1}{2}\left( n \right)}\\{x = - 1\left( l \right)}\end{array}} \right..\)

Bảng biến thiên:

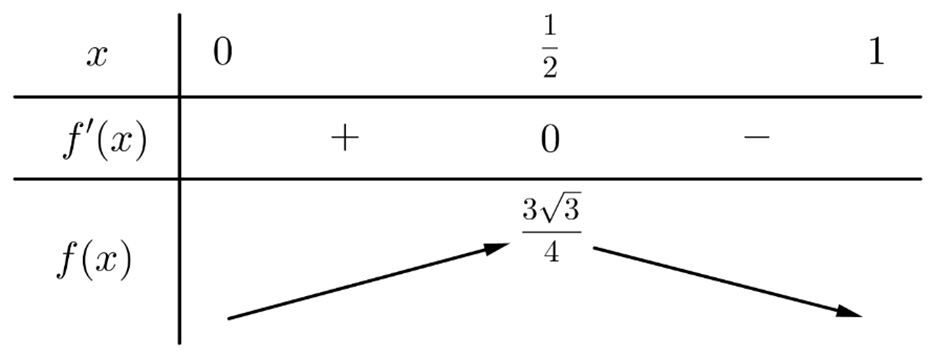
Dựa vào bảng biến thiên, ta thấy \(f\left( x \right) \le f\left( {\frac{1}{2}} \right) = \frac{{3\sqrt 3 }}{4}.\)

Vậy diện tích lớn nhất của hình thang \(ABCD\) là \(\frac{{3\sqrt 3 }}{4}\left( {{m^2}} \right).\)