Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8). Trong các khẳng định sau, khẳng định sai là A. BC = AD. B. ABCD là hình thang cân.
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).
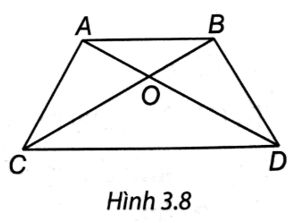
Trong các khẳng định sau, khẳng định sai là
A. BC = AD.
B. ABCD là hình thang cân.
C. AC = BD.
D. Tam giác AOC cân tại O.
