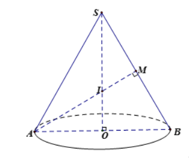
Cho hình nón có thiết diện qua trục là tam giác đều. Gọi V1,V2 lần lượt là thể tích của khối cầu nội tiếp và nội tiếp hình nón đã cho. Tính tỉ số

Trả lời

Giả sử cạnh của tam giác đều SAB bằng 1. Gọi thiết diện qua trục hình nón là tam giác đều SAB.

Gọi I là trọng tâm của tam giác đều SAB, khi đó I là tâm mặt cầu nội tiếp hình nón cũng là tâm mặt cầu ngoại tiếp hình nón.

Bán kính mặt cầu ngoại tiếp hình nón là: $R=SI=\frac{2}{3}SO=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}.$

Bán kính mặt cầu nội tiếp hình nón là: $r=IO=\frac{1}{3}SO=\frac{1}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{6}.$

Thể tích mặt cầu ngoại tiếp hình nón là: $V_1=\frac{4}{3}\text{π}{R}^3=\frac{4\sqrt{3}}{27}\text{π}.$

Thể tích mặt cầu nội tiếp hình nón là: $V_2=\frac{4}{3}\text{π}{r}^3=\frac{\sqrt{3}}{54}\text{π}.$

Vậy $\frac{V_1}{V_2}=8.$