Cho hình lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$  cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C'. Tính khoảng cách giữa hai đường thẳng MN và B'D'.

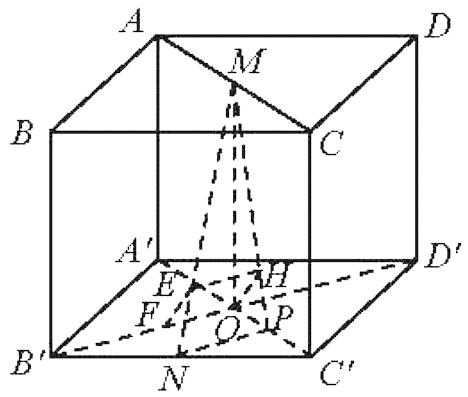
B'D' Ç A'C' tại O.

Gọi P là trung điểm của OC'.

Vě OH ^ MP, HE // NP, EF // OH.

ABCD là hình lập phương, ta dễ dàng có được: B'D' ^ (A'C'CA).

Hay B'D' ^ OH, mà OH // EF       

Þ EF ^ B'D' (1).

NP // B'D' Þ NP ^ (A'C'CA) hay NP ^ OH.

Đồng thời OH ^ MP.

Þ OH ^ (MNP) hay OH ^ MN Þ EF ^ MN (2)

Từ (1) và (2) ta có: d(MN, B'D') = EF = OH.

Xét tam giác vuông MOP, ta có OM = a, OP = $\frac{a\sqrt{2}}{4}$, suy ra OH = $\frac{a}{3}$ .

Vậy d(MN, B'D') = $\frac{a}{3}$