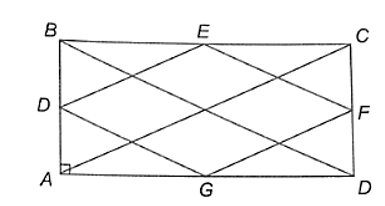
• Xét ∆ABC có: D, E lần lượt là trung điểm của AB và BC nên DE là đường trung bình của ∆ABC.

Suy ra $DE=\frac{1}{2}AC$ và DE // AC (tính chất đường trung bình của tam giác).

Xét ∆ADC có: G, F lần lượt là trung điểm của AD và CD nên GF là đường trung bình của ∆ADC.

Suy ra $GF=\frac{1}{2}AC$ và GF // AC (tính chất đường trung bình của tam giác).

Khi đó ta có $DE=GF=\frac{1}{2}AC$ và DE // GF // AC

Xét tứ giác DEFG có DE = GF và DE // GF nên DEFG là hình bình hành.

• Xét ∆ABD có: G là trung điểm AD; D là trung điểm AB nên GD là đường trung bình của ∆ABD.

Suy ra $DG=\frac{1}{2}BD$ (tính chất đường trung bình của tam giác).

Mà ABCD là hình chữ nhật nên AC = BD

Do đó $\frac{1}{2}AC=\frac{1}{2}BD$ hay DE = DG.

Hình bình hành DEFG có DE = DG nên là hình thoi.

Chú ý:Ngoài cách trên, ta có thể chứng minh DEFG là hình thoi bằng cách chứng minh bốn cạnh bằng nhau: $DE=FG=\frac{1}{2}AC=\frac{1}{2}BC=EF=GD.$