Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.

a) Tính khoảng cách từ S đến mặt phẳng (ABC).

b) Tính khoảng cách từ M đến mặt phẳng (SAG).

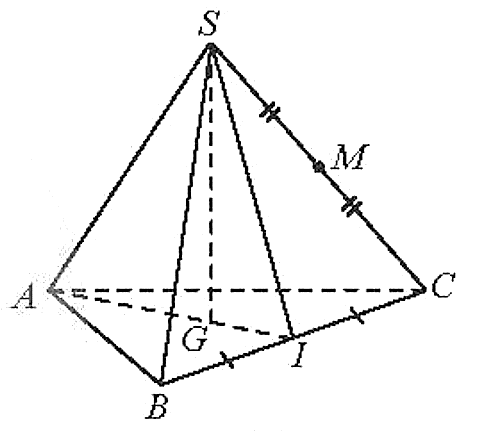
a) Do S.ABC là hình chóp tam giác đều nên SG ^ (ABC) hay d(S, (ABC))=SG.

Tam giác ABC là tam giác đều cạnh 3a nên

$AG=\frac{2}{3}.\frac{3a\sqrt{3}}{2}=a\sqrt{3}$

Tam giác SAG vuông tại G nên $SG=\sqrt{S{A}^2-A{G}^2}=\sqrt{4a^2-3a^2}=a$

Vậy d(S, (ABC)) = a.

b) Vì SC Ç (SAG) = S nên $\frac{d(M,(SAG\left)\right)}{d(C,(SAG\left)\right)}=\frac{MS}{CS}=\frac{1}{2}$

$\Rightarrow d(M,(SAG\left)\right)=\frac{1}{2}d(C,(SAG\left)\right)$

Gọi I là trung điểm của BC.

Ta có: CB ^ AI và CB ^ SG

Þ CB ^ (SAG) và CB Ç (SAG) = I.

Do đó $d(C,(SAG\left)\right)=CI=\frac{1}{2}BC=\frac{3a}{2}$

Vậy $d(M,(SAG\left)\right)=\frac{3a}{4}$