Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M,N lần lượt là trung điểm của SA,SC. Mặt phẳng (BMN) cắt SD tại P. Tỉ số VS.BMPN/VS.ABCD bằng: A. VS.BMPN/VS.ABCD = 1/16 B. VS.BMPN/VS.AB
37
30/04/2024
Cho hình chóp \(S.ABCD\)đáy là hình bình hành. Gọi \(M,N\)lần lượt là trung điểm của \(SA,SC\). Mặt phẳng \((BMN)\)cắt \(SD\)tại \(P\). Tỉ số \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}}\)bằng:
A. \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}} = \frac{1}{{16}}\).
B. \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}} = \frac{1}{6}\).
C. \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}} = \frac{1}{{12}}\).
D. \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}} = \frac{1}{8}\).
Trả lời
Lời giải
Chọn B
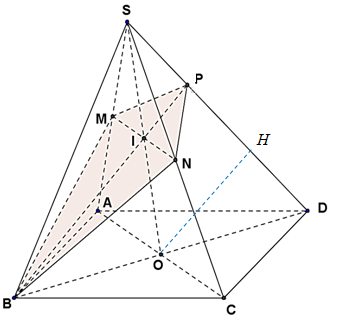
Ta có \(M,N\)là trung điểm của \(SA,SC\)nên \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SC}} = \frac{1}{2}\).
Cách 1: Áp dụng định lý Menelaus cho \(\Delta SOD\)ta có :\[\frac{{PS}}{{PD}} \cdot \frac{{BD}}{{BO}} \cdot \frac{{IO}}{{IS}} = 1 \Rightarrow \frac{{PS}}{{PD}} \cdot 2 \cdot 1 = 1 \Rightarrow \frac{{PS}}{{PD}} = \frac{1}{2} \Rightarrow \frac{{SP}}{{SD}} = \frac{1}{3}\].
Cách 2: Kẻ \(OH//BP\), ta có \(O\)là trung điểm của \(BD\)nên \(H\)là trung điểm của \(PD\).
Ta có \(OH//IP\)mà \(I\)là trung điểm của \(SO\)nên \(P\)là trung điểm của \(SH\).
Suy ra \(SP = PH = HD\)\[ \Rightarrow \frac{{SP}}{{SD}} = \frac{1}{3}\].
Theo công thức tỉ số thể tích ta có : \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}} = \frac{{2{V_{S.BMP}}}}{{2{V_{S.BAD}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SP}}{{SD}} = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}.\)
