Cho hình chóp S.ABCD có thể tích V. Gọi M, N lần lượt là trung điểm của SA, MC. Thể tích của khối chóp N.ABCD là A. V/4 B. V/2 C. V/3 D. V/6
47
04/05/2024
Cho hình chóp \(S.ABCD\) có thể tích \(V\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(SA\), \(MC\). Thể tích của khối chóp \(N.ABCD\) là
A. \(\frac{V}{4}\).
B. \(\frac{V}{2}\).
C. \(\frac{V}{3}\).
D. \(\frac{V}{6}\).
Trả lời
Lời giải
Chọn A
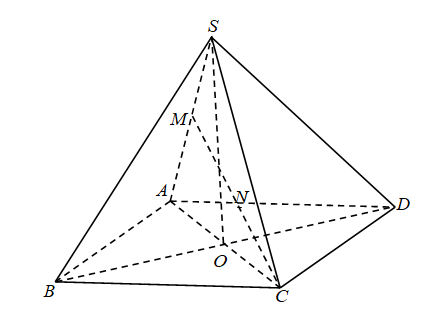
Đặt \(B = {S_{ABCD}}\), \(d\left( {S;\left( {ABCD} \right)} \right) = h\). Suy ra \(V = \frac{1}{3}Bh\).
Vì \(M\) là trung điểm của \(SA\) nên \(d\left( {M;\left( {ABCD} \right)} \right) = \frac{1}{2}d\left( {S;\left( {ABCD} \right)} \right)\),
Lại vì \(N\) là trung điểm của \(MC\) nên \(d\left( {N;\left( {ABCD} \right)} \right) = \frac{1}{2}d\left( {M;\left( {ABCD} \right)} \right)\).
Suy ra \(d\left( {N;\left( {ABCD} \right)} \right) = \frac{1}{4}d\left( {S;\left( {ABCD} \right)} \right) = \frac{1}{4}h\).
Từ đó ta có \({V_{N.ABCD}} = \frac{1}{3}d\left( {N;\left( {ABCD} \right)} \right).B = \frac{1}{4}.\frac{1}{3}Bh = \frac{V}{4}\).

