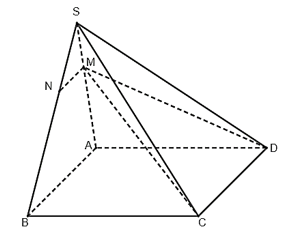
Cho hình chóp S.ABCD có đáy là hình bình hành. Trên cạnh SA lấy điểm M sao cho MA = 2MS. Mặt phẳng (CDM) cắt SB tại N. Tỉ số $\frac{SN}{SB}$ bằng:

Đáp án đúng là: B

Vì ABCD là hình bình hành nên AB // CD.

Ta có M ∈ SA nên M ⊂ (SAB).

Hai mặt phẳng (SAB) và (MCD) có M là điểm chung và lần lượt chứa hai đường thẳng AB và CD song song với nhau nên giao tuyến của chúng là đường thẳng đi qua M và song song với AB.

Từ M, kẻ đường thẳng song song với AB, cắt SB tại N. Khi đó (SAB) ∩ (MCD) = MN.

Do vậy N là giao điểm của SB và mặt phẳng (MCD).

Ta có MA = 2MS $\Rightarrow \frac{SM}{SA}=\frac{1}{3}$.

Xét tam giác SAB có MN // AB, theo định lí Thalés ta có: $\frac{SN}{SB}=\frac{SM}{SA}=\frac{1}{3}$.