Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, BC, CD.
a) Xác định giao điểm của đường thẳng NP với mặt phẳng (SAB).
b) Xác định giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SAB), (SAD), (SBC), (SCD).
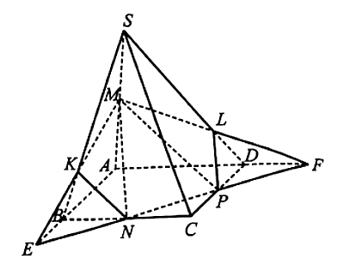
a) Vì N ∈ BC và P ∈ CD nên NP ⊂ (ABCD).
Trong mặt phẳng (ABCD), gọi E là giao điểm của NP và AB.
Ta có E thuộc AB nên E nằm trên mặt phẳng (SAB).
Vậy E là giao điểm của đường thẳng NP với mặt phẳng (SAB).
b)
+ Theo câu a) ta có E là một điểm chung của hai mặt phẳng (MNP) và (SAB).
Lại có M ∈ SA nên M ∈ (SAB) và M ∈ (MNP) nên M là điểm chung của hai mặt phẳng (MNP) và (SAB).
Do đó, giao tuyến của mặt phẳng (MNP) với mặt phẳng (SAB) là đường thẳng ME.
+ Trong mặt phẳng (ABCD), gọi F là giao điểm của NP và AD nên F là một điểm chung của mặt phẳng (MNP) với mặt phẳng (SAD).
Lại có M ∈ SA nên M ∈ (SAD) và M ∈ (MNP) nên M là một điểm chung của mặt phẳng (MNP) với mặt phẳng (SAD).
Khi đó, giao tuyến của mặt phẳng (MNP) với mặt phẳng (SAD) là đường thẳng MF.
+ Trong mặt phẳng (SAB), gọi K là giao điểm của ME và SB; trong mặt phẳng (SAD), gọi L là giao điểm của MF và SD. Khi đó, giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SBC), (SCD) lần lượt là các đường thẳng NK và PL.